이 포스트에서는

암호학을 조금이라도 이해하기 위한 기초를 다루는 포스트의 첫번째 단계입니다.

정수론(기초)#

1. 최대공약수(Greatest Common Divisor)#

최대공약수를 알기 위해서는 약수(Divisor) 를 알아야한다. 약수는 자연수 A, B가 있을 때, 두 수 A, B를 나누어 떨어지게 만드는 수를 말한다.

최대공약수는 당연히 그 약수 중 제일 큰 수를 말한다.

자! 근데 우리는 A, B가 주어졌을 때 어떻게 최대공약수를 알 수 있을까???

직관적이게 구현해볼까요??

a, b = map(int, input().split())
result = []
for i in range(1, max(a, b)+1):
    if a % i == b % i == 0: result.append(i)

print(result[-1])

자 이렇게 최대공약수를 얻는 코드를 작성해보았습니다.

그런데 이 코드는 O(max(a, b))의 시간복잡도를 가지고 있죠?? 하지만 암호학에서는 진짜 뭔 말도 안되는 큰 수들이 왔다갔다 거립니다…

이보다 더 빠른 알고리즘을 설계해 볼까요?

이때 사용할 알고리즘은 무엇이냐! 바로 유클리드 호제법(Euclidean algorithm) 을 사용할 겁니다!

유클리드 호제법

2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이 성질에 따라, b를 r로 나눈 나머지 r’를 구하고, 다시 r을 r’로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다.

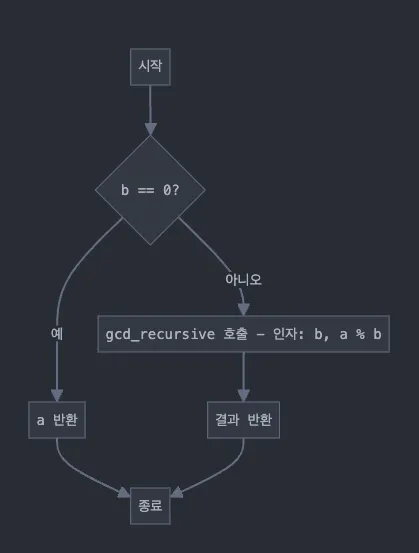
요런 유클리드 호제법을 구현해볼까?

def gcd_1(a, b):
    while b != 0: a, b = b, a % b
    return a
def gcd_2(a, b): # 함수 오버헤드 때문에 약간 느릴 수도
    return a if not b else gcd_2(b, a % b)

유클리드 호제법을 사용한 최대공약수(GCD) 알고리즘의 시간 복잡도는 ${O(\log(\min(a, b)))}$ 이죠? 굉장히 효율적입니다.

GCD를 이용한 최소공배수(LCM) 구하기

def lcm(a, b):
    return abs(a * b) // gcd(a, b) # overflow를 방지하기 위해서는 a*b를 분리해서 계산하면 됨.

2. 나머지 연산(Modular Arithmetic)#

나머지.. 우리는 % 연산자를 이용해서 나머지르 가져오죠? 그래서 % 연산을 mod 연산이라고 합니다.

그래서 이제 뭘 할거냐? 자 여러분 자연수 % 자연수는 너무나 쉽게 할 수 있겠죠..?

그러나 -12 % 7 은 어떻게 계산하실 거죠??

우리는 다음과 같은 규칙을 알아야 합니다.

• 결과는 항상 0이상이고, 나누는 수(예시에서는 7이죠?) 미만이어야 한다.
• (나누어지는 수) = (몫) * (나누는 수) + (나머지) 의 관계가 성립한다.

이거는 사실 중학교 때 배우는 것이긴 합니다..

그래서 -12 % 7의 과정을 얘기해 보겠습니다.

1. -12를 7로 나눈 몫을 구한다. -> -1.xxxx (소수점 내림)
2. -12 = -2 * 7 + 2

2번의 과정이 왜 나오냐!

• 2 % 7 = 2
• (2+7) % 7 = 2
• (7*2+2) % 7 = 2
• (7*n+2) % 7 = 2

-> 그래서 (7-2+2) = 2 이런 답이 나오게 됩니다.

이때 a % n = b % n인 경우, a와 b는 mod n에 대해여 **“합동”**이라고 합니다. 우리는 이걸 다음과 같게도 나타낼 수 있습니다. a ≡ b % n

ex) 19 ≡ 10 mod 9입니다. 그러면 19와 10은 9로 나눴을 때의 나머지는 1이기 때문에 요렇게 되지요!

이제는 큰 수를 나머지 연산을 취해볼겁니다!#

91^17 % 9을 계산해 보자!

계산

(91 + 9n) % 9 = 1
n = 0 -> 91 % 9 = 1
91 % 9 = 1 % 9 -> 91 ≡ 1 % 9
91^17 % 9 = 1 ^ 17 % 9 = 1

여기서 주목해야 할 것은 91 ≡ 1 % 9인 경우에 91을 1로 치환해도 이 연산이 성립한다는 개념입니다. 또 mod 연산은 분리도 가능합니다.

a+b mod n = (a mod n + b mod n) mod n 이런식으로 할 수 있습니다.

그래서 우리는 정수에 대한 모듈러 연산의 결과값들의 집합을 다음과 같이 정의할 수 있습니다.

$\mathbb{Z}_n={0,1,\ldots,(n-1)}$

이번 포스트에서는 여기까지 다루겠습니다.