[Algorithm] 벡터(Vector)

안녕하세요! 오늘은 수학의 핵심 개념인 벡터(Vector) 에 대해 알아보려고 합니다. 벡터는 물리학, 컴퓨터 그래픽스, 공학에서 필수적! 그냥 컴퓨터 하시면 알아야될 놈이구요. 이번 포스팅에서는 벡터의 개념과 기본적으로 알아두면 많이 쓸 외적, 내적 등에 대해서 알아보겠습니다.

1. 벡터란 무엇인가?#

벡터는 크기(magnitude) 와 방향(direction) 을 모두 가진 양을 의미합니다. 일상생활에서 예를 들자면

”북쪽으로 5km” (방향: 북쪽, 크기: 5km)
“시속 60km로 동쪽으로 이동” (방향: 동쪽, 크기: 시속 60km)

이런 정보들이 모두 벡터로 표현될 수 있습니다.

반면에 스칼라(scalar)는 크기만 있고 방향이 없는 양입니다

온도: 25°C
질량: 5kg
시간: 3시간

1.1 벡터의 수학적 표현#

수학적으로 벡터는 여러 방식으로 표현할 수 있습니다

화살표 표기법: $v$
좌표 표기법:
- 2차원: $v = (x, y)$
- 3차원: $v = (x, y, z)$
- n차원: $v = (x_{1}, x_{2}, ..., x_{n})$

1.2 벡터의 기본 연산#

벡터의 크기(norm)#

벡터 $v = (x, y, z)$ 의 크기는 다음과 같이 계산합니다

$∣ v ∣ = x^{2} + y^{2} + z^{2}$

벡터의 덧셈#

두 벡터 $a = (a_{1}, a_{2}, a_{3})$ 와 $b = (b_{1}, b_{2}, b_{3})$ 의 덧셈

$a + b = (a_{1} + b_{1}, a_{2} + b_{2}, a_{3} + b_{3})$

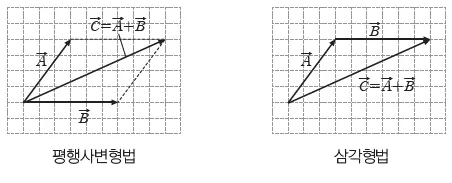
addition
출처 : 힘과 평형

덧셈의 기하학적 의미는 두 벡터를 이어붙이는 것 입니다. 첫 번째 벡터의 끝에서 두 번째 벡터를 이어서 그리면, 시작점에서 최종 도착점까지의 벡터가 두 벡터의 합이 됩니다 . 이를 “삼각형 법칙” 또는 “평행사변형 법칙”이라고 합니다.
(이거는 아마 제가 배우는 당시 2015 교육과정에서는 물2 에서 배웠던 걸로 기억합니다.)

벡터의 뺄셈#

두 벡터 $a = (a_{1}, a_{2}, a_{3})$ 와 $b = (b_{1}, b_{2}, b_{3})$ 의 뺄셈

$a - b = (a_{1} - b_{1}, a_{2} - b_{2}, a_{3} - b_{3})$

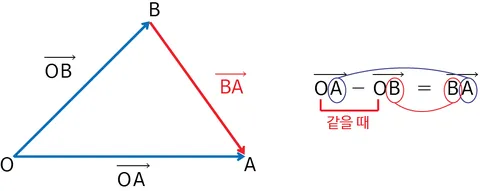
subtraction
출처 : 벡터의 뺄셈

뺄셈의 기하학적 의미는 벡터 $a$ 에서 벡터 $b$ 로의 변화 입니다. 두 점 사이의 방향과 거리를 나타내는 벡터를 구할 때 자주 사용되는 걸로 알고 있어요.

스칼라 곱셈#

벡터 $v$ 에 스칼라 $k$ 를 곱한 결과는

$k v = (k x, k y, k z)$

스칼라 곱셈은 벡터의 크기를 $k$ 배 변화시킵니다.

단위 벡터(Unit Vector)#

크기가 1인 벡터를 단위 벡터라고 합니다. 임의의 벡터 $v$ 를 단위 벡터로 변환하는 과정을 정규화(normalization) 라고 합니다. 아래와 같이 계산할 수 있습니다.

$\hat{v} = \frac{v}{∣ v ∣}$

단위 벡터는 방향만 중요할 때 유용하게 사용됩니다. 이거는 아마 인공지능 아니면 게임 개발할 대 많이 보셨던 것들이라 익술할거라고 생각합니다.(물론 하셨던 분들에게만)

2. 벡터의 내적(Dot Product)#

벡터의 내적은 두 벡터의 방향 관계와 크기를 모두 고려한 연산으로, 매우 중요한 개념입니다!

2.1 내적의 정의#

두 벡터 $a = (a_{1}, a_{2}, a_{3})$ 와 $b = (b_{1}, b_{2}, b_{3})$ 의 내적은

$a \cdot b = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}$

또는 크기와 각도를 이용해서..

$a \cdot b = ∣ a ∣∣ b ∣ cos θ$

여기서 $θ$ 는 두 벡터 사이의 각도입니다.

좀 더 깊게!

좀 더 공부좀 해오겠씁니다… ㅠ //: # () //: # (### 2.2 내적의 기하학적 의미)

3. 벡터의 외적(Cross Product)#

외적은 3차원 공간에서 두 벡터에 수직인 새로운 벡터를 생성하는 연산입니다.

3.1 외적의 정의#

두 벡터 $a = (a_{1}, a_{2}, a_{3})$ 와 $b = (b_{1}, b_{2}, b_{3})$ 의 외적은

$a \times b = (a_{2} b_{3} - a_{3} b_{2}, a_{3} b_{1} - a_{1} b_{3}, a_{1} b_{2} - a_{2} b_{1})$

행렬식으로도 계산할 수 있습니다

a \times b = i a_{1} b_{1} j a_{2} b_{2} k a_{3} b_{3}

여기서 $i$ , $j$ , $k$ 는 x, y, z축 방향의 단위 벡터입니다.

또한 외적의 크기는 다음과 같이 계산할 수 있습니다 $∣ a \times b ∣ = ∣ a ∣∣ b ∣ sin θ$

여기서 $θ$ 는 두 벡터 사이의 각도입니다.

좀 더 깊게!

좀 더 공부를…

지금 채워지지 않은 내용들은 추후에 업데이트 하겠습니다.

사실 CCW 포스팅하려고 하다가 그것보다 벡터를 선행적으로 포스팅하는게 좋다고 생각되어 이렇게 오게되었는데.. 이거 하다보니 이제는 행렬도 해야겠다는 생각이 드네요!

모두 수고하셨습니다!