[RL] Q-Learning 이론 - Compy's Blog

Q-Learning의 배경#

1980년대 후반, 강화학습 연구에서 가장 큰 도전으로는 “환경 모델을 모르는 상황에서도 최적 정책을 학습하는 것”이였습니다. 이때까지만해도 사용되던 알고리즘이 Dynamic Programming(이하 DP)였는데, 이 DP는 전이 확률과 보상 함수가 완전히 알려진 경우에만 사용이 가능해서 실제 문제에 적용하기가 어려웠습니다.

그래서 이러한 한계를 극복하기 위해서 model-free 알고리즘인 Q-learning을 개발하였습니다. 이 Q-learning은 model-free 강화학습의 가장 기초이며 핵심이 되는 알고리즘이 된답니다.

Q-learning 아이디어#

환경 모델이 없는 상태에서 최적 정책을 학습할 수 있도록 하는 것이 아이디어입니다. 기존 DP에서 $P (s ’∣ s, a)$ 와 보상 함수 R(s, a)를 필요로 했다면, Q-learning은 실제 경 (s, a, r, s’)만으로 Q-value를 업데이트합니다.

그래서 Q-learning의 핵심은 행동-가치 함수 Q(s, a)를 직접 학습하는 것입니다. 이제부터 이 함수를 Q함수라고 부르겠습니다.

이 Q함수는 상태 s에서 행동 a를 취한 후 최적 정책을 따를 때의 기대 누적 보을 나타냅니다. 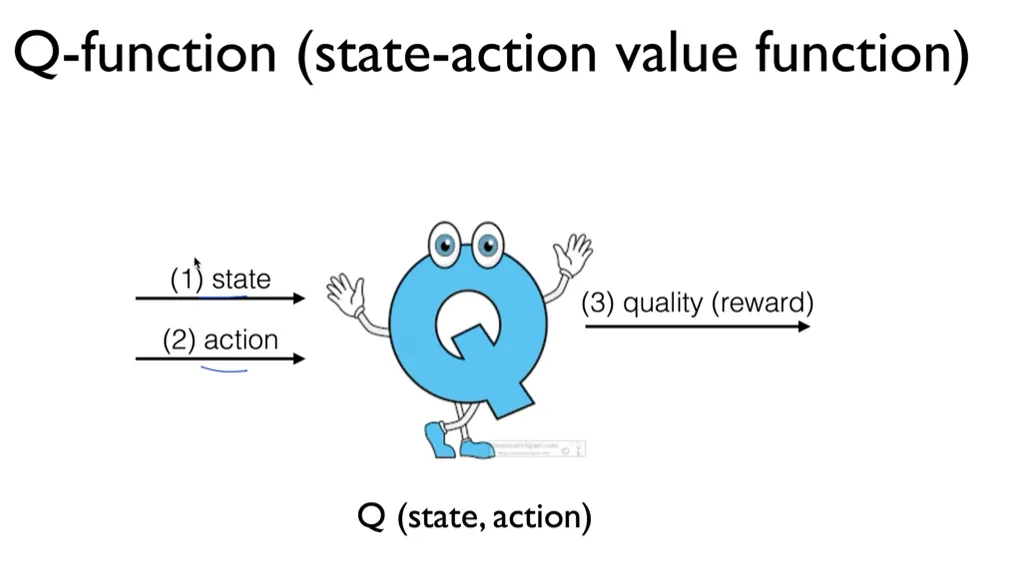Q-function

$Q^{*} (s, a) = R (s, a) + γ \sum_{s^{'}} P (s^{'} ∣ s, a) max_{a^{'}} Q^{*} (s^{'}, a^{'})$

$벨만 최적 방정식$

수식에 대해서 조금 더 설명을 더해보자면, $P (s^{'} ∣ s, a)$ 은 전이확률로 상태 s에서 행동 a를 했을 때, 상태 s`가 될 확률을 말합니다. $max_{a^{'}} Q^{*} (s^{'}, a^{'})$ 는 다음으로 될 상태 $s^{'}$ 에서 선택할 수 있는 행동 중에 가장 높은 Q-value를 의미합니다.

그래서 $\sum_{s^{'}} P (s^{'} ∣ s, a) max_{a^{'}} Q^{*} (s^{'}, a^{'})$ 이 부분은 다음 상태에서 얻을 수 있는 최적 가치의 기댓값으로 다음 상태에서 최선의 선택을 할 때 얻을 가치들의 확률적 평균으로 생각하면 되겠습니다.

즉, 벨만 최적 방정식은 Q-value를 계산하는 수식으로 $R (s, a) (현재 즉시 제공되는 보상)$ 과 $γ (할인 인자, discount factor)$ 가 곱해진 미래 가치 기댓값과의 합을 의미합니다.

Q-learning의 업데이트 규칙은 벨만 방정식과 시간차 학습(Temporal Difference Learning)을 기반으로 합니다. 조금 더 자세히 들어가자면, Q-learning의 업데이트 규칙은 벨만 최적 방정식의 해를 찾기 위해 시간차 학습을 활용하고, 매 스탭마다 TD error를 계산, Q-value를 업데이트 해갑니다. 이를 통해서 벨만 최적 방정식을 근사합니다.

$Q (s, a) \leftarrow Q (s, a) + α [r + γ max_{a^{'}} Q (s^{'}, a^{'}) - Q (s, a)]$

$Q-Learning 업데이트 규칙$

업데이트 규칙에서는 $α$ 는 학습률, $r$ 은 관찰된 즉시 보상, $γ$ 는 할인 인자이고, 대괄호 안의 항은 시간차 오차(TD Error)로, 현재 추정값과 실제 경험 사이의 차이를 나타냅니다.

Q-learning 특징#

1. off-policy 학습 가능#

off-policy 학습이 가능하다는 소리는 무슨 소리냐? 학습하려는 목표 정책과 실제 행동을 정하는 행동 정책이 다를 수 있음을 말합니다.

좀 더 자세히 설명하자면, Q-learning은 $ϵ$ -greedy와 같은 탐험적 정책을 사용해 데이터를 수집하면서도, greedy 정책에 대한 Q-value를 학습할 수 있다는 의미입니다.

2. 수렴성 조건#

먼저 수렴성을 조사하기 위해서 학습률 조건을 따져봐야합니다.

상태-행동 쌍에 대한 학습률의 총합은 무한대로 발산하며, 학습률 제곱의 총합은 윤한한 값으로 수렴해야됩니다.
모든 상태에서 모든 가능한 행동을 마훈히 반복적으로 경험해야됩니다.
Q-value는 개별적인 상태-행동 쌍에 대해 테이블 형태(look-up table)로 표현 가능해야합니다.

이정도가 있고요. 자세한 설명과 수식을 보고 싶으시면 아래 reference에 survey를 참고해주세요. 하튼 그리하여 이러한 조건 하에서 Q-learning은 확률 1로 최적 Q-function로 수렴합니다.

3. 탐험 전략#

보통 예제나 많이 사용되는 알고리즘으로 꼽히는게 $ϵ$ -greedy입니다.

ε-greedy 정책: 확률 ε로 무작위 행동을, (1-ε)로 탐욕적 행동을 선택하는 알고리즘

π (a ∣ s) = {1 - ϵ + \frac{ϵ}{∣ A ∣} \frac{ϵ}{∣ A ∣} if a = ar g max_{a^{'}} Q (s, a^{'}) otherwise

식으로는 위와 같이 표현 가능합니다.

그 외 정책들을 보고 싶으시면 똑같이 reference에서 survey를 참고해주세요.

4. 한계#

한계로는 확장성 문제, 연속 공간의 한계, 샘플 효율성, 수렴 속도 문제가 있습니다.

확장성 문제: 상태 공간과 행동 공간이 클 경우 Q-table의 크기가 기하급수적으로 증가하여 메모리와 계산 시간 측면에서 실용적이지 않음
연속 공간의 한계: 연속적인 상태나 행동 공간에서는 Q-table 표현 자체가 불가능하여 함수 근사가 필수적
샘플 효율성: 모든 상태-행동 쌍을 충분히 탐험해야 하므로 샘플 효율성이 낮음
수렴 속도 문제: 이론적으로는 수렴이 보장되지만, 큰 상태 공간에서는 실용적인 시간 내에 수렴하지 않을 수 있음

이렇게 정리할 수 있겠습니다.

Reference#

[1] J. H. Lee (compy), “Reinforcement Learning: A Survey,” compy’s Blog, Aug. 10, 2025. [Online]. Available: URL

[2] C. J. C. H. Watkins and P. Dayan, “Technical Note: Q-Learning,” Machine Learning, vol. 8, no. 3, pp. 279-292, May 1992, doi: 10.1023/A:1022676722315.