1. Introduction#

강화학습(Reinforcement Learning)은 에이전트가 환경과의 상호작용을 통해 최적의 행동 정책을 학습하는 기계학습의 한 분야이다. 전통적인 지도학습이나 비지도학습과 달리, 강화학습은 명시적인 정답 없이 환경으로부터의 보상 신호만을 통해 시행착오를 반복하며 학습을 수행한다. 강화학습의 핵심 개념은 1950년대 동물 심리학과 최적 제어 이론에서 시작되어, Bellman의 동적 계획법(Dynamic Programming)[30]과 Sutton & Barto의 시간차 학습(Temporal Difference Learning)[32] 등을 통해 이론적 기반이 확립되었다. 특히 1990년대 이후 Q-learning[2], Policy Gradient[18] 등의 알고리즘이 개발되면서 실용적 응용의 가능성이 크게 확장되었다. 최근 딥러닝과의 결합을 통한 Deep Reinforcement Learning의 등장은 강화학습 분야에 혁신적 발전을 가져왔다. 2013년 DeepMind의 DQN(Deep Q-Network)[4]이 Atari 게임에서 인간 수준의 성능을 달성한 것을 시작으로, 2016년 AlphaGo[9]가 바둑에서 프로 바둑기사를 격파하면서 강화학습의 잠재력이 전 세계적으로 주목받게 되었다. 현재 강화학습은 게임 AI를 넘어서 로보틱스[1], 자율주행, 금융, 추천시스템, 자원 관리, 의료, 자연어처리 등 다양한 분야에 적용되고 있다. 특히 복잡하고 동적인 환경에서 순차적 의사결정이 필요한 문제들에서 기존 방법론들보다 우수한 성능을 보이고 있어, 인공지능의 핵심 기술 중 하나로 자리잡았다. 본 논문은 robotics, optimization, environment simulation, game 등 다양한 영역을 포괄하며, 실제 적용 사례를 체계적으로 검토한다. 매일 발표되는 수많은 최신 연구들은 특정 세분화된 문제를 해결하기 위한 복잡한 기법들을 제시하고 있어, 연구자들이 최신 연구 동향을 파악하는 것이 점점 어려워지고 있다. 따라서 본 논문은 이러한 정보의 홍수 속에서 명확한 방향성을 제시하고자 한다. 강화학습의 근본이 되는 핵심 알고리즘에서부터 이들이 어떻게 최신 기술로 확장되었는지 체계적으로 분석하여, 독자들에게 구조화된 지식의 틀을 제공한다. 또한 이를 통해 강화학습 분야의 현황을 이해하고 미래의 발전 가능성을 전망하고자 한다.

2. Background#

1. 강화학습#

강화학습(Reinforcement Learning, RL)은 본질적으로 환경과의 시행착오적 상호작용을 통해 목표 지향적 행동을 학습하는 계산적 연구 분야로 정의할 수 있다[32].

핵심 목표#

강화학습의 핵심 목표는 수치적 보상 신호를 최대화하기 위해, 주어진 상황에서 무엇을 해야 할지, 즉 상황을 행동에 어떻게 연결할지를 학습하는 것이다[32].

에이전트(Agent) 라 불리는 학습 주체는 자신의 행동이 환경에 미치는 영향을 관찰(Observe) 하고, 그 결과로 주어지는 보상(Reward) 이라는 피드백을 통해 자신의 행동 전략을 점진적으로 개선해 나간다[32].

1.1. 구성요소#

강화학습 시스템은 두 가지 주요 관점에서 구성요소를 파악할 수 있습니다. 시스템 수준 과 에이전트 내부 수준이 있다.

시스템 수준 구성요소#

에이전트-환경 인터페이스#

강화학습의 가장 기본적인 모델은 에이전트(Agent)와 환경(Environment) 간의 상호작용 으로 구성된다[32]. 이 상호작용은 이산적인 시간 단위에 따라 순환적으로 발생한다.

시간 t에서 에이전트는 환경의 상태$S_t$를 관찰한다. 관찰된 상태를 바탕으로 하나의 행동$A_t$를 선택하면, 환경은 보상$R_{t+1}$을 부여하고 새로운 상태$S_{t+1}$로 전이된다[32].

핵심 구성 요소 정의#

구성요소	기호	설명
에이전트	-	학습의 주체이자 의사결정자. 환경을 관찰하고, 행동을 선택하며, 보상을 통해 학습
환경	-	에이전트와 상호작용하는 외부 세계. 에이전트의 행동을 입력으로 받아 새로운 상태와 보상을 출력
상태	$S,s$	특정 시점의 환경에 대한 정보. 의사결정에 필요한 모든 정보를 담고 있음
행동	$A,a$	에이전트가 특정 상태에서 선택할 수 있는 행위
보상	$R,r$	에이전트의 행동 결과에 대한 즉각적인 피드백을 나타내는 스칼라 값

에이전트 내부 구성요소#

1. 정책$(Policy,\pi )$#

에이전트의 행동 방식을 결정하는 핵심 구성요소로, 상태를 행동으로 매핑하는 함수이다[32].

정책은 결정론적 정책과 확률론적 정책으로 나눌 수 있습니다. 결정론적 정책$a=\pi (s)$는 주어진 상태에 대해 항상 특정 행동을 선택하는 반면, 확률론적 정책$\pi (a|s)=P(A_t=a|S_t=s)$는 각 행동에 대한 확률 분포를 제공한다[32].

2. 가치 함수$(ValueFunction)$#

미래에 대한 예측을 담당하는 구성요소로, 특정 상태 또는 상태-행동 쌍에서 기대되는 미래 보상의 총량을 추정한다[32].

가치 함수는 상태-가치 함수와 행동-가치 함수로 구분된다. 상태-가치 함수$(v_{\pi }(s))$는 정책$\pi$하에서 상태 s의 가치(이득의 기댓값)를 나타내며, 행동-가치 함수$(q_{\pi }(s,a))$는 상태 s에서 정책$\pi$를 따라 행동 a를 선택하는 것의 가치를 의미한다[32].

보상과 가치의 관계#

보상이 문제의 궁극적인 목표를 정의한다면, 가치 함수는 실제 의사결정 과정에서 가장 중요한 역할을 수행한다[32]. 에이전트는 즉각적인 보상만을 보고 행동을 선택하는 것이 아니라, 가장 높은 가치를 가질 것으로 추정되는 상태로 전이시키는 행동을 선택한다[32].

3. 모델 (Model)#

강화학습에서 모델(Model)이라는 것은 환경(Environment)에 대한 모델이다. 즉, 환경의 작동 방식을 모방하는 에이전트의 선택적 내부 구성요소이다[32]. 모델링을 하는 일반적인 이유는 불확실한 것에 대한 예측에 있다. 환경에 대한 모델이 있으면, 에이전트가 어떤 행동을 행했을 때의 결과를 예측할 수 있다[32]. 이를 정책 업데이트에 활용할 수도 있습니다. 가장 효율적으로 정책을 업데이트하는 상황만을 뽑아 정책을 활용할 수도 있다. 대표적으로 AlphaZero가 이 방법을 채택하고 있다[14], [17]. 이러한 모델을 이용하는 방법을 강화학습 알고리즘을 Model-Based 방법이라고 한다[15], [16].

만약 모델링이 정확하지 않은 상황이라면, 모델을 사용하지 않는게 더 효율적일 수 있다. 이때 모델없는 강화학습 알고리즘 Model-Free 방법이라고 한다 [2], [3].

1.2. MDP(Markov Decision Process)#

마르코프 속성#

MDP 프레임워크 전체를 관통하는 가장 근본적인 가정은 마르코프 속성(Markov Property) 이다[32]. 시스템의 미래가 오직 현재 상태와 현재 행동에만 의존하며, 과거의 모든 역사와는 무관하다는 것을 의미한다[32].

$P(S_{t+1}|S_t,A_t)=P(S_{t+1}|S_t,A_t,S_{t-1},A_{t-1},...,S_0,A_0)$

$\text{[수식 2.1] 마르코프 속성}$

이 속성의 핵심은 ‘상태가 미래를 예측하는 데 필요한 모든 정보를 담고 있는 충분 통계량’이라는 점이다[32].

MDP의 정형적 정의#

마르코프 결정 과정은 수학적으로 5-tuple$(S,A,P,R,\gamma )$로 정의된다[32].

• 상태 공간(State Space) S: 환경에서 가능한 모든 상태들의 집합
• 행동 공간(Action Space) A: 각 상태에서 에이전트가 선택할 수 있는 모든 행동들의 집합
• 전이 확률(Transition Probability) P:$P(s^{\prime }|s,a)=P(S_{t+1}=s^{\prime }|S_t=s,A_t=a)$로 정의되는 상태 전이 확률
• 보상 함수(Reward Function) R:$R(s,a)$또는$R(s,a,s^{\prime })$로 표현되는 즉시 보상
• 할인 인자(Discount Factor) γ:$\gamma \in [0,1]$로, 미래 보상의 현재 가치를 조절하는 매개변수

이러한 정의를 통해 강화학습 문제를 명확한 수학적 프레임워크 내에서 다룰 수 있게 된다[32].

정책과 가치 함수#

MDP에서 에이전트의 행동 전략은 정책(Policy)으로 표현된다[32]. 정책은 각 상태에서 어떤 행동을 선택할지를 결정하는 규칙이며, 결정론적 정책$\pi (s)=a$와 확률론적 정책$\pi (a|s)$로 구분된다[32].

정책의 성능을 평가하기 위해 가치 함수(Value Function) 개념이 도입된다[32]. 상태-가치 함수는 특정 정책을 따를 때 해당 상태에서 기대되는 누적 할인 보상을 나타낸다:

$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[{\sum }_{t=0}^{\infty }{\gamma }^t{R}_{t+1}|S_0=s\right]$

$\text{[수식 2.2] 상태-가치 함수}$

행동-가치 함수는 특정 상태에서 특정 행동을 선택한 후 정책$\pi$를 따를 때의 기대 누적 보상을 의미한다[32]:

$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }\left[{\sum }_{t=0}^{\infty }{\gamma }^t{R}_{t+1}|S_0=s,A_0=a\right]$

$\text{[수식 2.3] 행동-가치 함수}$

벨만 방정식#

가치 함수들 사이의 재귀적 관계는 벨만 방정식(Bellman Equation) 으로 표현된다[30,32]. 이는 현재 상태의 가치를 즉시 보상과 다음 상태의 할인된 가치의 합으로 분해한 것이다[30].

상태-가치 함수에 대한 벨만 방정식은 다음과 같다:

$V^{\pi }(s)={\sum }_a\pi (a|s){\sum }_{s^{\prime }}P(s^{\prime }|s,a)\left[R(s,a)+\gamma V^{\pi }(s^{\prime })\right]$

$\text{[수식 2.4] 상태-가치 함수의 벨만 방정식}$

행동-가치 함수에 대한 벨만 방정식은 다음과 같이 표현된다:

$Q^{\pi }(s,a)={\sum }_{s^{\prime }}P(s^{\prime }|s,a)\left[R(s,a)+\gamma {\sum }_{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })\right]$

$\text{[수식 2.5] 행동-가치 함수의 벨만 방정식}$

최적 정책과 수렴성#

MDP의 궁극적 목표는 최적 정책(Optimal Policy)${\pi }^{\ast }$를 찾는 것이다[32]. 최적 정책은 모든 상태에서 최대 가치를 달성하는 정책으로 정의된다.

${\pi }^{\ast }(s)=\arg {\max }_a{Q}^{\ast }(s,a)$

$\text{[수식 2.6] 최적 정책}$

최적 가치 함수들은 최적 벨만 방정식(Optimal Bellman Equation) 을 만족한다[30,32].

$V^{\ast }(s)={\max }_a{\sum }_{s^{\prime }}P(s^{\prime }|s,a)\left[R(s,a)+\gamma V^{\ast }(s^{\prime })\right]$

$\text{[수식 2.7] 최적 상태-가치 함수의 벨만 방정식}$

$Q^{\ast }(s,a)={\sum }_{s^{\prime }}P(s^{\prime }|s,a)\left[R(s,a)+\gamma {\max }_{a^{\prime }}{Q}^{\ast }(s^{\prime },a^{\prime })\right]$

$\text{[수식 2.8] 최적 행동-가치 함수의 벨만 방정식}$

중요한 점은 유한한 MDP에서는 항상 최적 정책이 존재하며[32], 벨만 최적화 연산자는 수축 매핑의 성질을 가져 유일한 해로 수렴한다는 것이다[30]. 이러한 이론적 보장은 강화학습 알고리즘들의 수렴성 분석에 핵심적인 역할을 한다[32].

MDP의 기본 가정과 한계#

MDP 프레임워크는 몇 가지 중요한 가정들을 전제로 한다[32]. 완전 관측 가능성(Full Observability) 은 에이전트가 환경의 완전한 상태 정보에 접근할 수 있다고 가정한다. 정적 환경(Stationary Environment) 가정은 전이 확률과 보상 함수가 시간에 따라 변하지 않는다고 본다. 또한 이산 시간(Discrete Time) 구조를 가정하여 의사결정이 순차적인 시간 단계에서 이루어진다고 본다.

이러한 가정들은 실제 환경에서 종종 위배될 수 있다[32]. 많은 실제 문제들은 부분 관측만 가능하거나(POMDP), 연속적인 상태와 행동 공간을 가지거나, 환경이 시간에 따라 변화하는 특성을 보인다. 또한 상태 공간이 클 경우 차원의 저주(Curse of Dimensionality) 문제가 발생하여 함수 근사 기법의 도입이 필수적이 된다[32].

1.3. 탐험 vs. 활용#

다른 학습에서 찾아볼 수 없는 강화학습만이 갖는 어려운 점은 탐험 과 활용 사이를 절충하는 일이다[32].

활용(Exploitation)은 현재까지의 정보를 바탕으로 최선의 결정을 내리는 행위로, 즉각적인 기대 보상을 최대화하는 것을 의미한다[32]. 반면 탐험(Exploration)은 현재로서는 최선이 아니라고 생각되는 행동을 시도하여 더 많은 정보를 수집하는 행위로, 단기적 보상을 희생하지만 장기적으로 더 나은 전략 발견이 가능한다[32].

많은 보상을 얻기 위해서 에이전트는 과거에 보상을 획득하는 데 효과적이었던 행동들을 선호해야만 한다[32]. 그러나 이런 최적의 행동을 발견하려면 과거에 하지 않았던 행동들을 시도해 봐야한다. 즉, 에이전트는 보상을 얻기 위해 이미 경험한 행동들을 활용해야 하지만, 한편으로는 미래에 더 좋은 행동을 선택하기 위한 탐험을 해야만 하는 것이다[32]. 순수한 활용만을 추구하는 에이전트는 초기에 발견한 국소 최적해에 갇혀 전역 최적해를 발견할 기회를 놓칠 수 있다[32].

탐험 전략#

탐욕적 방법(Greedy)은 항상 현재 추정된 행동-가치가 가장 높은 행동을 선택하는 방식이다[32]. 하지만 이 방법은 처음 발견한 괜찮은 행동에 고착되어 다른 가능성을 탐색하지 않는다는 문제점이 있다.

ε-그리디 방법은 작은 확률$\epsilon$로는 무작위 행동을 선택하여 탐험을 수행하고,$1-\epsilon$확률로는 현재 추정된 최선의 행동을 선택하여 활용을 수행하는 방식이다[32]. 이 방법은 구현이 간단하며 모든 행동이 샘플링될 기회를 보장한다는 장점이 있지만, 방향성 없는 탐험으로 인해 비효율적이라는 단점이 있다.

그 외에도 감쇠하는 엡실론과 신뢰 상한(UCB) 등의 확장된 이론들이 있다[32]. 감쇠하는 엡실론은 학습 초기에는 높은$\epsilon$으로 탐험을 장려하고 점진적으로$\epsilon$를 감소시키는 방법이며, 신뢰 상한(UCB)은 불확실성이 높은 행동에 보너스를 부여하여 지향성 있는 탐험을 수행하는 방법이다[32].

1.4. 딥러닝 기법#

강화학습 연구에서 빈번히 사용되는 핵심적인 신경망 구조들을 소개한다.

1.4.1. 합성곱 신경망 (Convolutional Neural Network, CNN)#

합성곱 신경망은 이미지와 같은 격자 구조 데이터를 효과적으로 처리하기 위해 설계된 신경망이다[25]. CNN의 핵심은 지역적 연결성(Local Connectivity) 과 매개변수 공유(Parameter Sharing) 를 통해 공간적 계층 구조를 학습하는 것이다[25].

합성곱 연산은 다음과 같이 정의된다:

$(f\ast g)(i,j)={\sum }_m{\sum }_{n}f(m,n)\cdot g(i-m,j-n)$

$\text{[수식 2.9] 합성곱 연산}$

여기서$f$는 입력 특징맵,$g$는 학습 가능한 필터(커널)이다[25]. 이후 풀링(Pooling) 연산을 통해 공간적 차원을 축소하면서 중요한 특징을 보존한다[25].

강화학습에서 CNN은 주로 시각적 관측을 처리하는 데 사용된다. DQN에서는 Atari 게임의 픽셀 입력을 처리하기 위해 여러 층의 합성곱층을 사용하여 게임 화면에서 중요한 시각적 패턴을 추출한다[4], [4-1].

1.4.2. 순환 신경망 (Recurrent Neural Network, RNN)#

순환 신경망은 시계열 데이터나 순차적 입력을 처리하기 위해 설계된 신경망이다. RNN의 핵심 특징은 내부 은닉 상태(Hidden State) 를 통해 과거 정보를 기억할 수 있다는 점이다.

기본 RNN의 동작은 다음과 같이 표현된다:

$h_t=\tanh (W_{hh}{h}_{t-1}+W_{xh}{x}_t+b_h)$

$\text{[수식 2.10] RNN 은닉 상태 업데이트}$

$y_t=W_{hy}{h}_t+b_y$

$\text{[수식 2.11] RNN 출력}$

여기서$h_t$는 시점$t$의 은닉 상태,$x_t$는 입력,$y_t$는 출력이며,$W$들은 학습 가능한 가중치 행렬이다.

실제로는 기울기 소실 문제를 해결하기 위해 LSTM(Long Short-Term Memory)이나 GRU(Gated Recurrent Unit) 같은 개선된 구조가 더 널리 사용된다. 강화학습에서 RNN은 부분 관측 환경에서 과거 관측들을 기억하거나, World Models에서와 같이 시간적 동역학을 모델링하는 데 활용된다[8].

1.4.3. 변분 오토인코더 (Variational Autoencoder, VAE)#

변분 오토인코더는 고차원 데이터를 저차원 잠재 공간으로 압축하면서 동시에 데이터의 확률적 생성 모델을 학습하는 생성 모델이다[13]. VAE는 인코더(Encoder) 와 디코더(Decoder) 로 구성되며, 잠재 변수에 확률적 해석을 부여한다[13].

VAE의 목적 함수는 다음과 같은 변분 하한(Variational Lower Bound)을 최대화한다[13]:

$\mathcal{L}(\theta ,\varphi ;x)={\mathbb{E}}_{q_{\varphi }(z|x)}[\log p_{\theta }(x|z)]-D_{KL}(q_{\varphi }(z|x)\Vert p(z))$

$\text{[수식 2.12] VAE 목적 함수 (변분 하한)}$

여기서 첫 번째 항은 재구성 손실(Reconstruction Loss) 로 입력 데이터를 얼마나 잘 복원하는지를 측정하고, 두 번째 항은 KL 발산 정규화 로 학습된 잠재 분포가 사전 분포(일반적으로 표준 정규분포)에 가깝도록 제약한다[13].

인코더는 입력$x$를 잠재 변수$z$의 평균과 분산으로 매핑하며, 재매개화 기법(Reparameterization Trick) 을 통해 확률적 샘플링 과정에서도 역전파가 가능하도록 한다[13]:

$z=\mu +\sigma \odot ϵ,ϵ\sim \mathcal{N}(0,I)$

$\text{[수식 2.13] 재매개화 기법}$

강화학습에서 VAE는 고차원 관측을 저차원 표현으로 압축하는 데 사용된다. World Models에서는 시각적 관측을 잠재 벡터로 인코딩하여 환경의 동역학 학습을 더 효율적으로 만든다[8]. 이를 통해 원시 픽셀 공간에서 직접 계획하는 것보다 훨씬 효과적인 학습이 가능하다[8].

1.5 Mathematical Notation#

기호	설명	영문명
$\mathcal{S}$	상태 집합	Set of states
$\mathcal{A}$	행동 집합	Set of actions
$\mathcal{A}(s)$	상태$s$에서 가능한 행동들의 집합	Set of actions possible in state$s$
$s,s^{\prime }$	상태	States
$a$	행동	Action
$r$	보상	Reward
$t$	시간 단계	Time step
$T$	최종 시간 단계 (에피소딕 태스크)	Final time step
$p(s^{\prime },r|s,a)$	환경 dynamics	Environment dynamics
$p(s^{\prime }|s,a)$	상태 전이 확률	State transition probability
$r(s,a)$	상태$s$에서 행동$a$의 기대 보상	Expected reward
$r(s,a,s^{\prime })$	상태 전이$(s,a,s^{\prime })$에 대한 기대 보상	Expected reward for transition
$\pi$	정책	Policy
$\pi (a|s)$	상태$s$에서 행동$a$를 선택할 확률	Stochastic policy
${\pi }_{\ast }(s)$	결정적 최적 정책	Deterministic optimal policy
${\pi }_{\ast }$	최적 정책	Optimal policy
$G_t$	시간$t$에서의 리턴	Return from time$t$
$\gamma$	할인율 ($0\le \gamma \le 1$)	Discount rate
$v_{\pi }(s)$	정책$\pi$하에서 상태$s$의 가치	State-value function under policy$\pi$
$q_{\pi }(s,a)$	정책$\pi$하에서 상태-행동 쌍의 가치	Action-value function under policy$\pi$
$v_{\ast }(s)$	최적 상태 가치 함수	Optimal state-value function
$q_{\ast }(s,a)$	최적 행동 가치 함수	Optimal action-value function
$\hat{v}(s,\mathbf{w})$	가중치 벡터$\mathbf{w}$를 가진 상태 가치 함수의 근사	Approximate state-value function
$\hat{q}(s,a,\mathbf{w})$	가중치 벡터$\mathbf{w}$를 가진 행동 가치 함수의 근사	Approximate action-value function
$\mathbf{w}$	가중치 벡터 (크리틱 매개변수)	Weight vector (Critic parameters)
$\mathbf{x}(s)$	상태$s$의 특성 벡터	Feature vector for state$s$
$\mathbf{x}(s,a)$	상태-행동 쌍$(s,a)$의 특성 벡터	Feature vector for state-action pair
$\alpha$	스텝사이즈 매개변수 (학습률)	Step-size parameter
${\delta }_t$	시간차 오차	Temporal-difference error
$V(s)$	상태 가치 추정치	Estimated state value
$Q(s,a)$	행동 가치 추정치	Estimated action value
$N(s)$	상태$s$의 방문 횟수	Number of visits to state$s$
$N(s,a)$	상태-행동 쌍$(s,a)$의 방문 횟수	Number of visits to state-action pair
$\mathbf{\theta }$	정책 매개변수 벡터	Policy parameter vector
$\pi (a|s,\mathbf{\theta })$	매개변수$\mathbf{\theta }$를 가진 정책	Parameterized policy
$J(\mathbf{\theta })$	정책 성능 측도	Policy performance measure
$\nabla J(\mathbf{\theta })$	성능 측도의 기울기	Gradient of performance measure
${\rho }^{\pi }(s)$	정책$\pi$하에서 상태$s$의 정상 분포	Stationary distribution under policy$\pi$
$I_t$	할인 인자 (${\gamma }^t$)	Discount factor
$ϵ$	탐험 확률 ($ϵ$-탐욕 정책에서)	Exploration probability
$\tau$	시간 상수 또는 추적 감쇠	Time constant or trace decay
$\lambda$	적격도 추적에서의 감쇠 매개변수	Eligibility trace decay parameter
${\mathbf{e}}_t$	적격도 추적 벡터	Eligibility trace vector
$d$	상태 또는 특성의 차원	Dimensionality

$\text{[표 1.1] 수학 표기표}$

3. Taxonomy#

강화학습 에이전트 연구들을 체계적으로 분류하고 분석하기 위해서, 본 논문에서는 학습 알고리즘 분류 체계를 제시한다.

$\text{[그림 3.1] 강화학습 알고리즘에 따른 분류}$

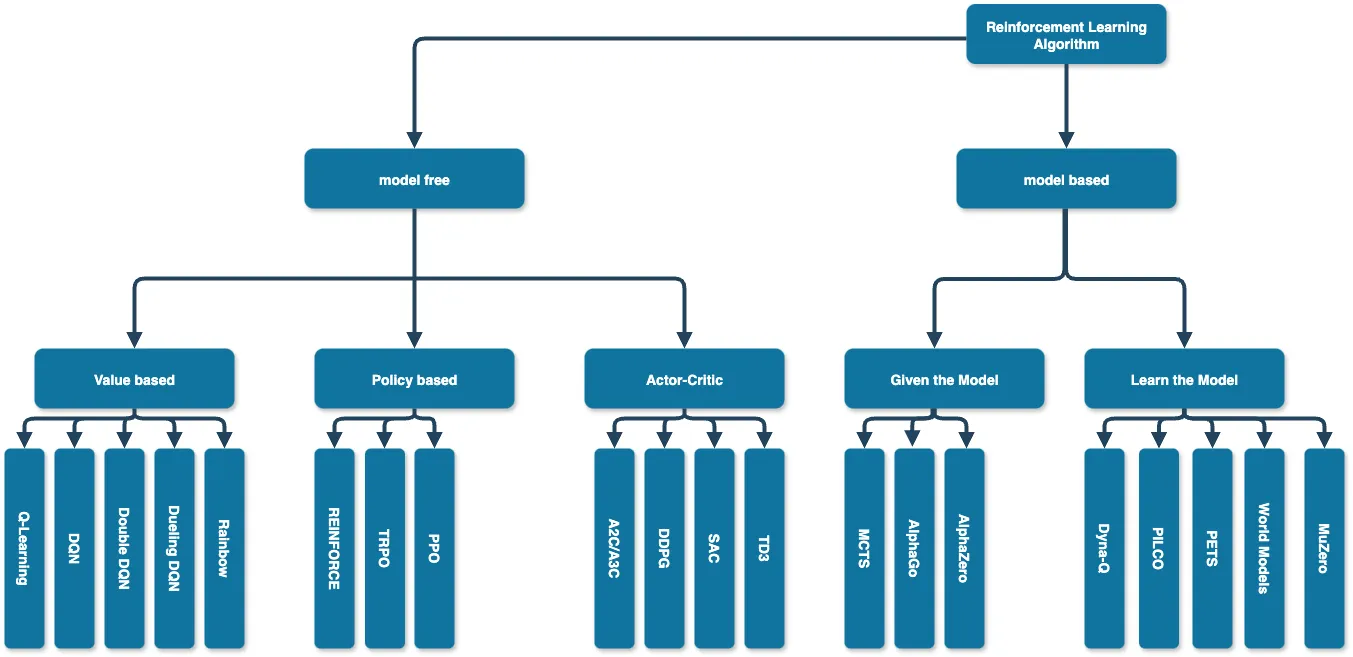
강화학습 알고리즘은 모델 유무에 따라 크게 모델을 활용하는 Model Based 와 모델을 활용하지 않는 Model Free 두가지로 나눌 수 있다 [32].

3.1. Model Based Algorithm#

Model Based 는 환경 정보량에 따라 Given the Model과 Learn the Model로 분류된다 [32].

3.1.1. Given the Model#

Given the Model은 환경의 전이 확률과 보상 함수가 완전히 알려진 경우로, 체스나 바둑과 같은 완전정보 게임에서 활용된다 [9] [14]. 이러한 환경에서는 모든 상태 전이와 결과를 정확히 예측할 수 있어 최적 계획 알고리즘을 직접 적용할 수 있다 [30].

3.1.2 Learn the Model#

반면 Learn the Model은 환경 모델이 사전에 주어지지 않지만 상호작용을 통해 학습 가능한 경우에 해당한다 [15]. 로보틱스나 자율주행과 같은 실제 환경에서는 물리 법칙이나 동역학 모델의 정확한 파라미터를 모르지만, 경험 데이터를 통해 환경 모델을 근사적으로 학습할 수 있습니다 [10] [16] [17]. 이 접근법은 학습된 모델의 부정확성이라는 추가적인 도전 과제를 수반한다.

3.2 Model Free Algorithm#

Model Free 는 무엇을 학습하냐에 따라 Value-Based, Policy-Based, Actor-Critic으로 분류된다 [32].

3.2.1 Value Based#

Value-Based 방법은 상태 가치 함수$V(s)$또는 행동 가치 함수$Q(s,a)$를 학습하여 간접적으로 정책을 도출한다. 학습된 가치 함수에서 greedy 또는 ε-greedy 정책을 통해 최적 행동을 선택하며, Q-learning [2], DQN [4] 등이 대표적이다. 이론적 수렴성이 보장되지만 연속 행동 공간 처리에 제약이 있다.

3.2.2 Policy Based#

Policy-Based 방법은 정책$\pi (a|s)$를 직접 파라미터화하여 학습한다. 정책 경사(policy gradient) 방법을 통해 기대 보상을 최대화하는 방향으로 정책을 개선하며 [18], REINFORCE [18], PPO [3] 등이 해당된다. 연속 행동 공간과 확률적 정책을 자연스럽게 다룰 수 있으나 높은 분산으로 인해 학습이 불안정할 수 있다.

3.2.3 Actor-Critic#

Actor-Critic은 정책(Actor)과 가치 함수(Critic)를 동시에 학습하는 방법이다. Actor는 정책을 학습하여 행동을 선택하고, Critic은 가치 함수를 학습하여 Actor의 성능을 평가한다. 이를 통해 Policy-Based 방법의 높은 분산 문제를 완화하면서도 두 방법의 장점을 결합할 수 있다. A2C [20], DDPG [21], SAC [22] 등이 대표적인 알고리즘이다.

4. Representative Works#

강화학습 분야의 발전은 이론적 기반을 확립하고 실용적 응용을 가능하게 한 핵심 연구들에 의해 이루어졌다. 본 섹션에서는 강화학습의 역사적 발전 과정에서 중요한 이정표가 된 다섯 가지 대표적인 연구를 심층 분석한다. 각 연구는 당시의 주요 문제를 해결하면서 새로운 연구 방향을 제시했으며, 현재까지도 강화학습 알고리즘 개발의 기초가 되고 있다.

4.0. Dynamic Programming (Bellman, 1957)#

4.1.1. 배경 및 동기#

1950년대 중반, 복잡한 다단계 의사결정 문제를 해결하기 위한 체계적인 수학적 프레임워크가 필요했다. 당시 존재하던 최적화 기법들은 단일 단계 결정이나 단순한 순차적 문제에만 적용 가능했고, 미래의 결정이 현재 결정에 영향을 미치는 복잡한 상황을 다루기에는 한계가 있었다. Richard Bellman은 이러한 문제를 해결하기 위해 동적 계획법(Dynamic Programming)을 제시했다 [30].

4.1.2. 알고리즘 설계#

4.1.2.1. 최적화 원리 (Principle of Optimality)#

Bellman의 가장 중요한 기여는 최적화 원리의 정립이다 [30]. 이 원리는 “최적 정책의 특성상, 초기 상태와 초기 결정이 무엇이든 상관없이, 나머지 결정들은 첫 번째 결정으로부터 얻어진 상태에 대한 최적 정책을 구성해야 한다”고 명시한다.

수학적으로 아래와 같이 표현된다:

$V^{\ast }(s)={\max }_a\left[R(s,a)+\gamma {\sum }_{s^{\prime }}P(s^{\prime }|s,a)V^{\ast }(s^{\prime })\right]$

$\text{[수식 4.1] 벨만 최적 방정식 (Bellman Optimality Equation)}$

[수식 4.1]에서$V^{\ast }(s)$는 상태$s$에서의 최적 가치 함수,$R(s,a)$는 즉시 보상,$\gamma$는 할인 인자,$P(s^{\prime }|s,a)$는 전이 확률을 나타낸다.

4.1.2.2. 벨만 방정식의 수학적 특성#

1. 고정점 정리 (Fixed Point Theorem): 최적 가치 함수는 벨만 최적화 연산자의 유일한 고정점이다 [32].
2. 수축 매핑 (Contraction Mapping): 할인 인자$\gamma <1$일 때, 벨만 연산자는 수축 매핑이 되어 수렴성을 보장한다 [32].
3. 동적 프로그래밍의 최적 부분구조: 전체 문제의 최적해가 부분 문제들의 최적해로 구성된다 [30].

4.1.2.3. 최적 정책 탐색 알고리즘#

4.1.2.3.1. 정책 반복 (Policy Iteration)#

• 정책 평가: 주어진 정책에 대한 가치 함수 계산
• 정책 개선: 탐욕적 정책 업데이트

정책 반복 알고리즘은 단순히 평가와 개선 이것을 반복하는 방법을 말한다 [32].

$\text{[그림 4.1] 정책 반복 알고리즘 의사코드 (Policy Iteration Pseudocode)}$

정책 반복은 정책 평가 단계가 수렴할 때까지 계속 진행되기 때문에 시간이 오래걸리는 한계가 있다. 즉, 정책 평가에서 발생하는 많은 sweep이 문제이다 [32].

4.1.2.3.2. 가치 반복 (Value Iteration)#

가치 반복은 정책 반복에서 정책 평가의 sweep의 횟수를 줄인 방법이다 [32]. 정책 평가 단계에서 수렴시키지 않고 바로 한 번의 sweep만 진행한 후 정책 개선을 시키는 방법으로 문제를 개선하였다. 평가와 개선을 한 번의 sweep으로 결합한 방법이 가치 반복이다 [32].

$\text{[그림 4.2] 가치 반복 알고리즘 의사코드 (Value Iteration Pseudocode)}$

4.1.2.3.3. 정책 반복 vs. 가치 반복#

$\text{[그림 4.3] 정책 반복과 가치 반복의 그리드 환경 수렴 비교}$

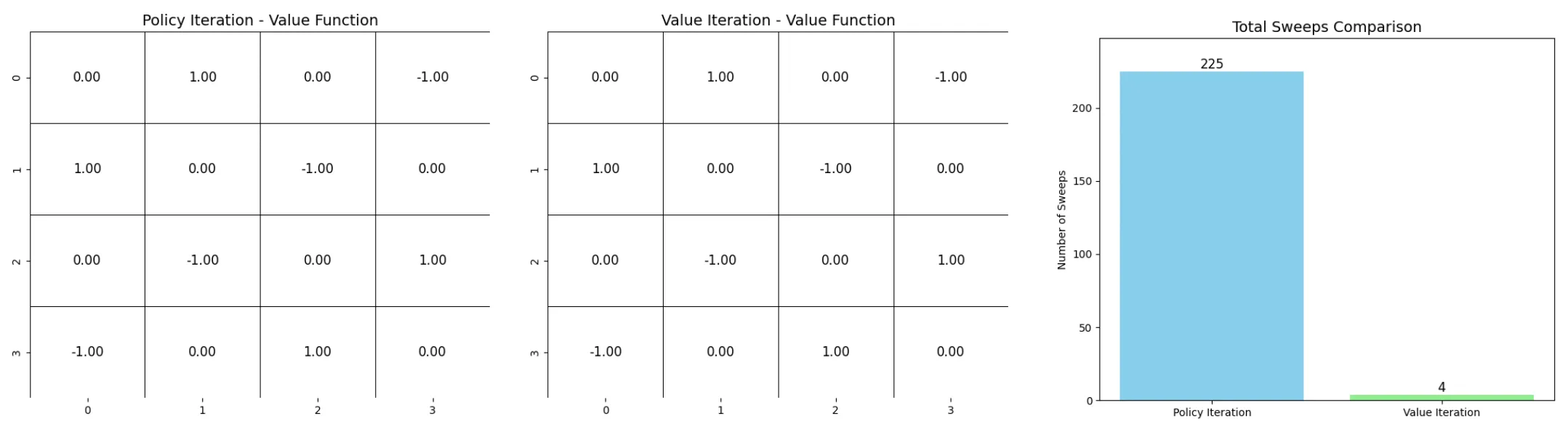
Grid 공간을 통해서 두 방법을 비교했다. 왼쪽 상단(0,0)이 출발점, 오른쪽 하단(3, 3)이 도착점이다. 바깥으로 나가는 경우는 없으며, 동서남북으로 이동 가능하다. 출발점과 도착점은 1의 보상, 제외한 다른 위치는 -1의 보상을 갖다. 할인 인자는 1로 그대로 유지하도록 한다.

이때 sweep의 수와 수렴한 결과를 보면 가치 반복이 정책 반복보다 효율적인 것을 확인할 수 있다.

4.1.3. 한계#

동적 계획법의 계산 복잡도는 상태 공간과 행동 공간의 크기에 직접적으로 의존한다 [30]. $n$개의 상태와$m$개의 행동이 있는 경우, 각 반복에서$O(n^{2}m)$의 계산이 필요하다. 이는 상태 공간이 큰 실제 문제에서 “차원의 저주(Curse of Dimensionality)“라는 근본적인 한계를 야기한다[30].

4.1.4. 학문적 의의#

Bellman의 동적 계획법은 현재까지도 강화학습의 이론적 기반으로 활용되고 있다[32]. MDP(Markov Decision Process) 프레임워크, 가치 함수의 개념, 최적성 조건 등은 모두 Bellman의 연구에서 비롯되었으며, Q-learning[2], 정책 경사법[18], Actor-Critic[32] 등 모든 현대 강화학습 알고리즘의 이론적 토대가 되고 있다.

4.1. Model Based#

4.1.1. Given the Model#

4.1.1.1. MCTS(Monte Carlo Tree Search)#

MCTS (Monte Carlo Tree Search) 는 체스나 바둑과 같은 완전정보 게임에서 기존 minimax 알고리즘의 완전 탐색으로 인한 계산 비효율성 문제를 해결하기 위해 개발되었다 [29]. 바둑같은 게임에서 모든 경우의 수를 계산하는 것은 현실적으로 불가능에 가까웠기 때문에, 유망한 경로만 선택적으로 탐색하고 몬테카를로 시뮬레이션을 통해서 결과를 추정하는 방식을 도입했다.

$\text{[그림 4.4] MCTS 의사코드}$

MCTS는$Algorithm1$에서 확인할 수 있는 Selection, Expansion, Simulation, Backpropagation 단계를 순서대로 반복하며 가장 유망한 수를 찾아간다 [29].

$\text{[그림 4.5] UCB1(Upper Confidence Bound 1) 선택 정책 의사코드}$

Selection 단계에서는$Algorithm2$의 UCB1 선택 정책을 사용해 탐험과 활용의 균형을 맞추며 노드를 선택한다 [29]. Expansion 단계에서는 선택된 리프 노드에서 가능한 행동들 중 하나 이상의 자식 노드를 추가한다. Simulation(Playout) 단계에서는 새로 추가된 노드부터 게임이 끝날 때까지 랜덤 정책으로 시뮬레이션을 진행한다. Backpropgation 단계에서는 시뮬레이션 결과를 루트까지의 모든 경로 노드에 역전파하여 통계를 업데이트한다.

MCTS는 점근적 최적성이 보장되며 도메인 지식 없이도 동작하고 언제든지 중단 가능(anytime algorithm)하다 [29]. 하지만 여전히 계산이 복잡하며, 연속적인 행동 공간을 처리하기 힘들고, 수렴 속도가 느리다는 한계를 가지고 있다.

4.1.1.2. AlphaGo#

AlphaGo은 Monte Carlo Tree Search(MCTS)와 딥러닝을 결합하여 바둑에서 세계 정상급 성능을 달성하였으며, 이 과정에서 네 가지 주요 신경망을 활용한다 [9].

$\text{[그림 4.6] AlphaGo neural network 구조 및 훈련 과정}$

$p_{\sigma }(a|s)=\text{softmax}(f_{\sigma }(s))$

$\text{[수식 4.2] AlphaGo 지도학습 정책 네트워크}$

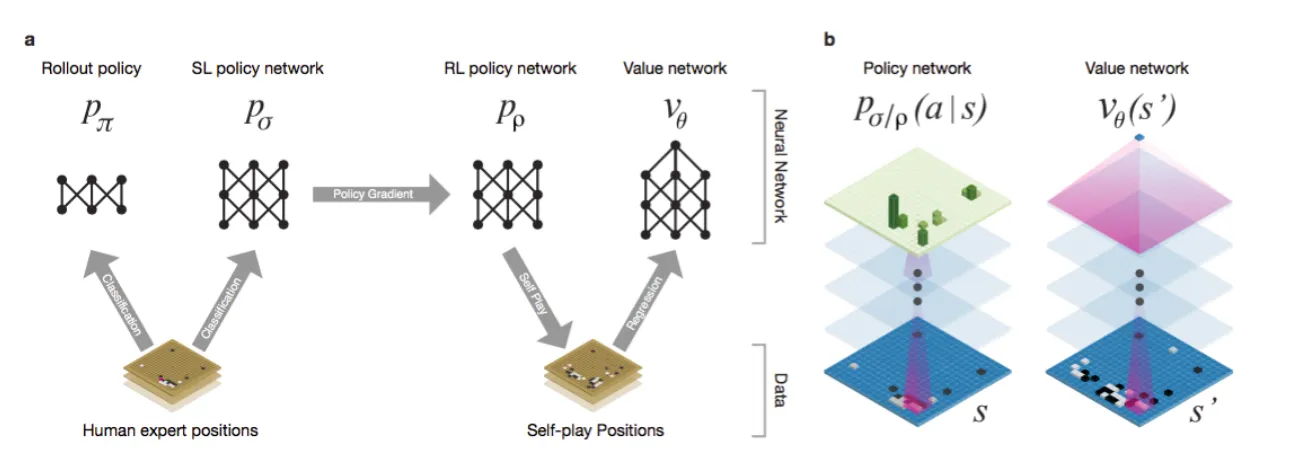
지도학습 정책 네트워크(Supervised Learning Policy Network) 는 [수식 4.2]로 정의되며, 대규모 인간 전문가 기보 데이터셋을 활용하여 전문가의 행동 패턴을 학습한다 [9]. 교차엔트로피 손실함수를 최적화하여 주어진 바둑판 상태 $s$에서 전문가가 선택할 가능성이 높은 행동$a$의 확률 분포를 근사하며, 이를 통해 바둑의 기본적인 전략적 원리와 휴리스틱을 내재화한다.

강화학습 정책 네트워크(Reinforcement Learning Policy Network) 는 $p_{\rho }(a|s)$로 표현되며, 지도학습으로 초기화된 정책을 기반으로 자기 대국(self-play) 환경에서 정책 기울기 방법을 통해 개선된다 [9].

$\Delta \rho =\alpha \frac{\partial \log p_{\rho }(a_t|s_t)}{\partial \rho }{z}_t$

$\text{[수식 4.3] 강화학습 정책 네트워크의 정책 매개변수 업데이트 규칙}$

정책 매개변수는 [수식 4.3]에 따라 업데이트되며,$z_t$는 최종 게임 결과의 보상 신호(승리 +1, 패배 -1)를 나타낸다. 이 과정을 통해 승률 최대화를 목표로 하는 최적 정책을 탐색한다.

$v_{\theta }(s)=\tanh (g_{\theta }(s))$

$\text{[수식 4.4] 바둑판에 대한 상태-가치 함수}$

가치 네트워크(Value Network) 는 [수식 4.4]를 근사하여 현재 위치에서의 게임 결과를 예측한다 [9]. 강화학습 정책의 self-play에서 생성된 위치-결과 쌍 데이터를 사용하여 MSE 손실함수로 훈련되며, 전통적인 MCTS의 무작위 시뮬레이션(random rollout) 기반 평가를 신경망 기반 평가로 대체함으로써 탐색 효율성과 추정 정확도를 향상시켰다.

$\text{[그림 4.7] AlphaGo-MCTS 의사코드}$

AlphaGo-MCTS는$Algorithm4$와 같이 기존 MCTS의 각 단계를 개선했다 [9].

선택(Selection) 단계에서는 UCB1에 정책 네트워크의 prior probability를 추가하고, 확장(Expansion) 단계에서는 정책 네트워크가 제안하는 유망한 수만 확장한다. 평가(Evaluation) 단계에서는 Random rollout 대신 가치 네트워크로 즉시 평가하며, 역전파(Backup) 단계에서는 가치 네트워크 결과를 역전파한다.

이를 통해 AlphaGo는 탐색 효율성이 크게 향상되고 인간 수준을 뛰어넘는 성능을 달성했지만, 인간 데이터에 의존하며 복잡한 파이프라인과 막대한 계산량이라는 단점을 가지고 있다 [9].

4.1.1.3. AlphaGo Zero#

AlphaGo Zero는 AlphaGo의 인간 데이터 의존성 문제를 해결하고 범용적 게임 AI를 구현하기 위해 개발되었으며, 단일 신경망과 순수 self-play 학습을 통해 체스, 쇼기, 바둑에서 동시에 superhuman 성능을 달성했다 [14] [17].

AlphaGo Zero 는 AlphaGo의 인간 데이터 의존성과 복잡성 문제를 해결하기 위해서 고안됐다 [14].

$\text{[그림 4.8] AlphaGo Zero self-play}$

$Algorithm5$에서 확인할 수 있듯 AlphaGo Zero 인간 기보 학습 단계를 완전히 제거하였으며, 백지 상태(tabula rasa)에서 self-play만으로 학습을 진행한다 [14]. 또한 단일 신경망 구조를$(p,v)=f_{\theta }(s)$을 채택하여 정책과 가치를 동시에 출력하는 하나의 네트워크를 사용하며, 공유된 representation learning으로 효율성을 증대시켰다 [14]. 여기서$p$는 각 행동에 대한 확률 분포, $v$는 현재 상태의 가치 추정,$f_{\theta }$는 신경망 함수를 의미한다.

$L=(z-v{)}^2-{\pi }^T\log p+c||\theta |{|}^2$

$\text{[수식 4.5] AlphaGo Zero 손실 함수}$

AlphaGo Zero의 학습 최적화는 [수식 4.5]를 통해 이뤄진다[14]. 여기서$z$는 실제 게임 결과(+1, 0, -1),$v$는 가치 네트워크 예측, $\pi$는 MCTS가 생성한 개선된 정책,$p$는 신경망의 정책 출력,$c$는 L2 정규화 계수를 의미한다.

AlphaGo Zero는 인간 편견 제거로 더 창의적인 전략 발견이 가능하고, 단순한 구조로 오히려 더 좋은 성능을 냈으며, 다양한 게임에 범용 적용이 가능하다 [14] [17]. 하지만 여전히 초기 학습 시간이 길고, 대용량 계산 자원이 필요하며, 완전정보 게임에만 제한된다는 한계가 존재한다.

4.1.2. Learn the Model#

4.1.2.1. Dyna-Q#

Dyna-Q는 Model Free 강화학습의 샘플 효율성 문제를 해결하기 위해서 등장했다 [15]. 실제 환경과의 상호작용은 비용이 크고 제한적이기 때문에, 경험을 통해 환경 모델을 학습하고 이 모델로 가상 경험을 대량으로 생성해 추가 학습에 활용하는 방법을 채택하였다.

$\text{[그림 4.8] Dyna-Q 의사코드}$

Dyna-Q는$Algorithm6$처럼 실제 경험으로 Q-function를 업데이트하는 동시에, 학습된 모델을 사용해 가상의 상태-행동-보상-다음상태 시퀀스를 생성하여 추가적인 Q-Learning 업데이트를 수행한다 [15].

$\hat{R}(s,a)=\text{observed reward from }(s,a)$

$\hat{T}(s,a)=\text{observed next state from }(s,a)$

$\text{[수식 4.6] Dyna-Q 알고리즘의 근사 함수 정의}$

환경 모델 학습을 위해 Dyna-Q는 위와 같이 관찰된 경험으로부터 보상 함수와 전이 함수를 근사한다. 여기서$\hat{R}(s,a)$는 상태-행동 쌍$(s,a)$에서 관찰된 보상이고,$\hat{T}(s,a)$는 상태-행동 쌍$(s,a)$에서 관찰된 다음 상태를 의미한다.

실제 경험 단계에서는 환경에서$(s,a,r,s^{\prime })$를 관찰하여 Q-table과 모델$(\hat{R},\hat{T})$를 업데이트한다.
계획 단계(planning) 에서는 학습된 모델을 사용하여 n번의 planning update를 수행하는데, 방문했던 상태-행동 쌍$(s,a)$를 무작위로 선택하고, 모델에서$r=\hat{R}(s,a)$,$s^{\prime }=\hat{T}(s,a)$를 생성한다. 이후 Q-Learning 업데이트를 수행한다 [15].

Dyna-Q는 실제 경험과 모델 기반 시뮬레이션을 결합하여 학습 효율성을 크게 향상시킨다. 그러나 모델의 오류가 누적되는 문제와 복잡한 환경에서 정확도가 저하되는 단점이 존재한다. 특히 환경이 변화하는 경우 부정확한 모델로 인해 성능이 악화될 수 있으며, deterministic 모델의 한계로 확률적 환경에서는 효과가 제한적이다 [15].

4.1.2.2. PILCO#

PILCO(Probabilistic Inference for Learning Control) 는 연속 제어 환경에서 샘플 효율성 문제를 해결하기 위해 개발되었다 [16]. 기존 강화학습 방법들이 많은 시행착오를 통해 천천히 학습하는 것과 달리, PILCO는 가우시안 프로세스를 활용하여 확률적 모델로 불확실성을 명시적으로 고려함으로써 적은 샘플로도 효과적인 학습을 가능하게 한다.

$\text{[그림 4.9] PILCO 의사코드}$

$Algorithm7$에서 확인할 수 있듯이, PILCO는 가우시안 프로세스 기반 동역학 모델링과 확률적 정책 최적화를 결합한다 [16].

$f(x)\sim \mathcal{G}\mathcal{P}(\mu (x),k(x,x^{\prime }))$

$J(\pi )={\mathbb{E}}_{\tau \sim p(\tau |\pi )}\left[{\sum }_{t=0}^{T-1}c(x_t,u_t)\right]$

$\text{[수식 4.7] 가우시안 프로세스 모델링에서의 동역학 함수}$

[수식 4.7]에서$f(x)$는 가우시안 프로세스로 모델링된 동역학 함수,$\mu (x)$는 평균 함수,$k(x,x^{\prime })$는 커널(공분산) 함수,$J(\pi )$는 정책$\pi$에 대한 기대 비용, $c(x_t,u_t)$는 시점 t에서의 즉시 비용을 의미한다.

PILCO의 주요 특징은 불확실성 전파를 통해 가우시안 프로세스를 통해 모델 불확실성을 명시적으로 추적하며, 해석적 계산에서는 가우시안 분포의 성질을 이용하여 기대값을 해석적으로 계산한다는 것이다 [16]. 또한 정책 최적화 과정에서는 기대 비용의 gradient를 계산하여 정책을 직접 최적화한다.

PILCO는 매우 적은 샘플로도 복잡한 제어 문제를 해결할 수 있다. 하지만 고차원 문제에서 계산 복잡도가 급격히 증가하고($O(n^3)$), 가우시안 가정의 한계로 복잡한 분포를 모델링하기 어렵다 [16]. 또한 커널 함수 선택에 민감하며 비가우시안 노이즈나 불연속성을 다루기 어렵다는 한계가 존재한다.

4.1.2.3. PETS#

PETS(Probabilistic Ensembles with Trajectory Sampling) 는 PILCO의 확장성 한계를 극복하기 위해 개발되었다 [10]. 가우시안 프로세스는 고차원에서 계산이 어려우므로, 신경망 앙상블을 사용해서 불확실성을 추정하면서도 복잡한 제어 문제를 처리할 수 있게 했다.

$\text{[그림 4.10] PETS 의사코드}$

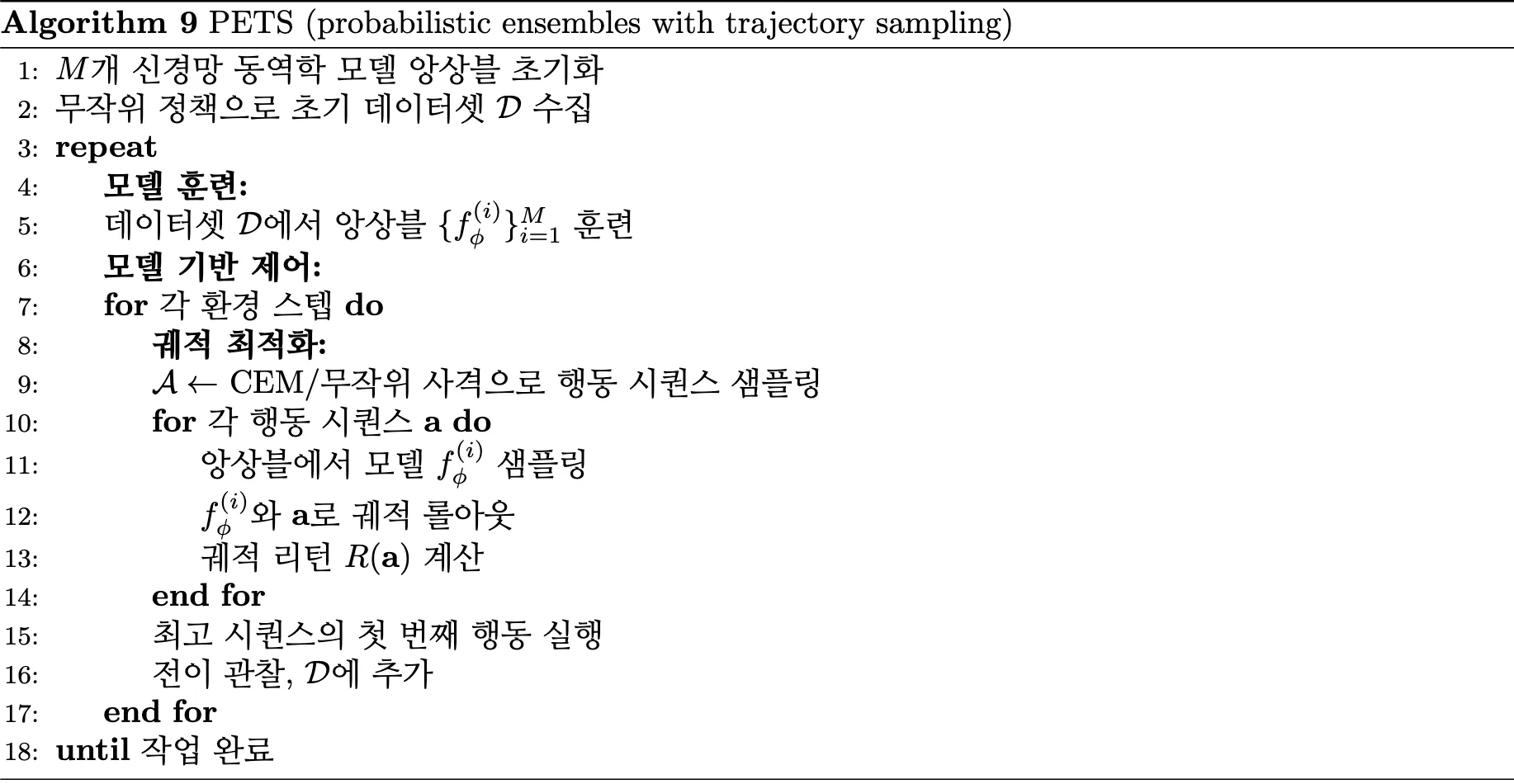
$Algorithm8$에서 확인할 수 있듯이, PETS는 앙상블 기반 모델 학습과 궤적 샘플링을 통한 계획을 결합한다.

${\hat{f}}_i(s_t,a_t)=s_{t+1}+{ϵ}_i,i=1,\dots ,E$

$\mu (s,a)=\frac{1}{E}{\sum }_{i=1}^E{\hat{f}}_i(s,a)$

${\sigma }^2(s,a)=\frac{1}{E}{\sum }_{i=1}^E({\hat{f}}_i(s,a)-\mu (s,a){)}^2$

$\text{[수식 4.8] PETS 앙상블 모델의 불확실성 추정}$

앙상블 모델 학습을 위해 PETS는 위와 같이 여러 신경망의 예측을 결합하여 불확실성을 추정한다. 여기서${\hat{f}}_i$는 i번째 앙상블 모델, $E$는 앙상블 크기,$\mu (s,a)$는 앙상블 평균(예측값),${\sigma }^2(s,a)$는 앙상블 분산(불확실성 추정)을 의미한다.

PETS의 핵심은 세 가지 구성요소로 이뤄진다 [10]. 앙상블 불확실성 추정에서는 여러 신경망의 예측 차이로 epistemic uncertainty를 추정하며, MPC 계획에서는 Model Predictive Control을 사용하여 유한 지평선에서 최적 행동을 계획하며, 궤적 샘플링(Trajectory Sampling) 에서는 앙상블에서 무작위로 모델을 샘플링하여 여러 가능한 궤적을 평가하고 robust한 정책을 학습한다.

PETS는 PILCO보다 확장성이 뛰어나면서도 불확실성을 고려한 안전한 학습이 가능하다 [10]. 그러나 모델 오류의 누적 문제와 앙상블 크기와 성능 간의 trade-off 문제가 여전히 존재한다. 앙상블이 클수록 계산 비용이 증가하고, 분포 외(out-of-distribution) 상황에서 불확실성 추정이 부정확할 수 있다. 또한 MPC의 지평선 길이에 따른 성능 민감도 문제도 존재한다.

4.1.2.4. World Models#

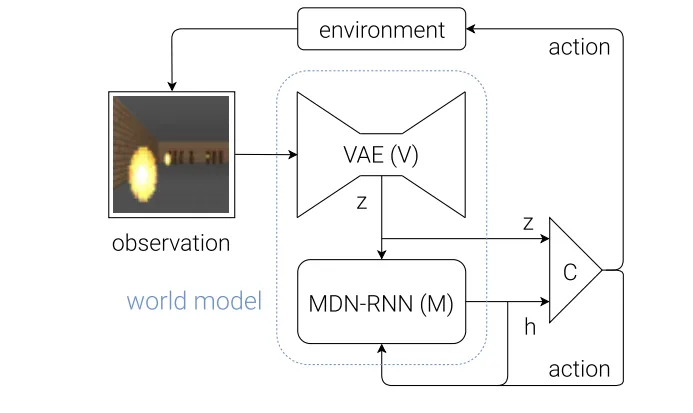
World Models는 복잡한 고차원 관측(이미지 등)에서 효율적으로 학습하는 문제를 다뤘다 [8]. VAE로 관측을 압축된 잠재 표현으로 변환하고, RNN으로 시간적 동역학을 학습하는 능력을 구현했다. 즉, 압축된 공간에서 상상 속 경험을 통해 학습할 수 있게 됐다.

$\text{[그림 4.11] World Model의 3가지 구성요소}$

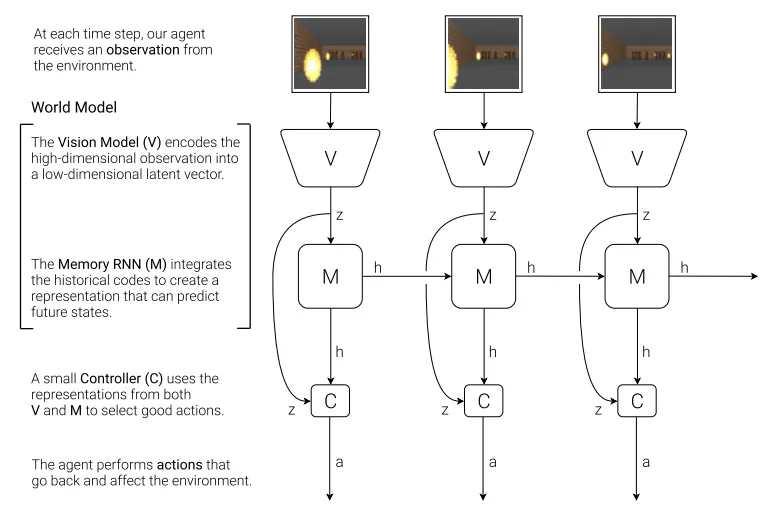
[그림 4.11]에서 확인할 수 있듯이, World Models는 세 가지 핵심 구성요소로 이루어져 있다 [8]. Vision Model(VAE) 는 관측$o_t$를 저차원 잠재 벡터$z_t$로 인코딩하여 복잡한 고차원 입력을 압축한다. Memory Model(MDN-RNN) 은 잠재 표현$z_t$와 행동$a_t$를 입력받아 은닉 상태$h_t$를 업데이트하며, 시간적 의존성과 부분 관측성을 처리한다. Controller(C) 는 Vision Model의 잠재 표현$z_t$와 Memory Model의 은닉 상태$h_t$를 결합하여 최적 행동을 선택하는 소형 신경망이다.

$\text{[그림 4.11] World Model의 Agent Model}$

Vision Model은 매 시점마다 고차원 관측 이미지를 32차원 잠재 벡터로 압축하여 핵심 특징을 추출한다 [13]. Memory RNN은 이전 시점의 은닉 상태와 현재 잠재 표현, 행동을 통합하여 환경의 동역학을 학습하고 미래 상태를 예측한다. Controller는 Vision Model과 Memory Model로부터 얻은 압축된 정보를 바탕으로 행동 공간에서 최적 정책을 실행한다. 이러한 분리된 구조를 통해 각 구성요소를 독립적으로 훈련할 수 있으며, 학습된 World Model 내에서 예측 경험을 생성하여 실제 환경과의 상호작용 없이도 안전하고 효율적으로 정책을 개선할 수 있다.

World Models는 시각적으로 복잡한 환경에서도 효율적인 학습을 가능하게 하며, 해석 가능한 잠재 표현을 통해 학습 과정을 시각화할 수 있다는 장점을 갖는다 [8]. 그러나 VAE의 정보 손실로 인한 중요한 세부사항 누락, 잠재 공간 품질에 대한 높은 의존성, RNN의 장기 의존성 한계, 그리고 복잡한 3단계 학습 과정(VAE → RNN → Controller)으로 인한 구현 및 튜닝의 어려움이라는 한계점들이 존재한다.

4.1.2.5. MuZero#

MuZero는 AlphaZero가 완전 정보 게임에만 적용 가능하다는 한계를 극복했다 [17]. 실제 환경 동역학을 학습하는 대신, 계획에 필요한 내부 표현만 학습하여 부분 관측이나 불완전 정보 환경에서도 효과적으로 작동할 수 있다.

$\text{[그림 4.13] MuZero Network 구조}$

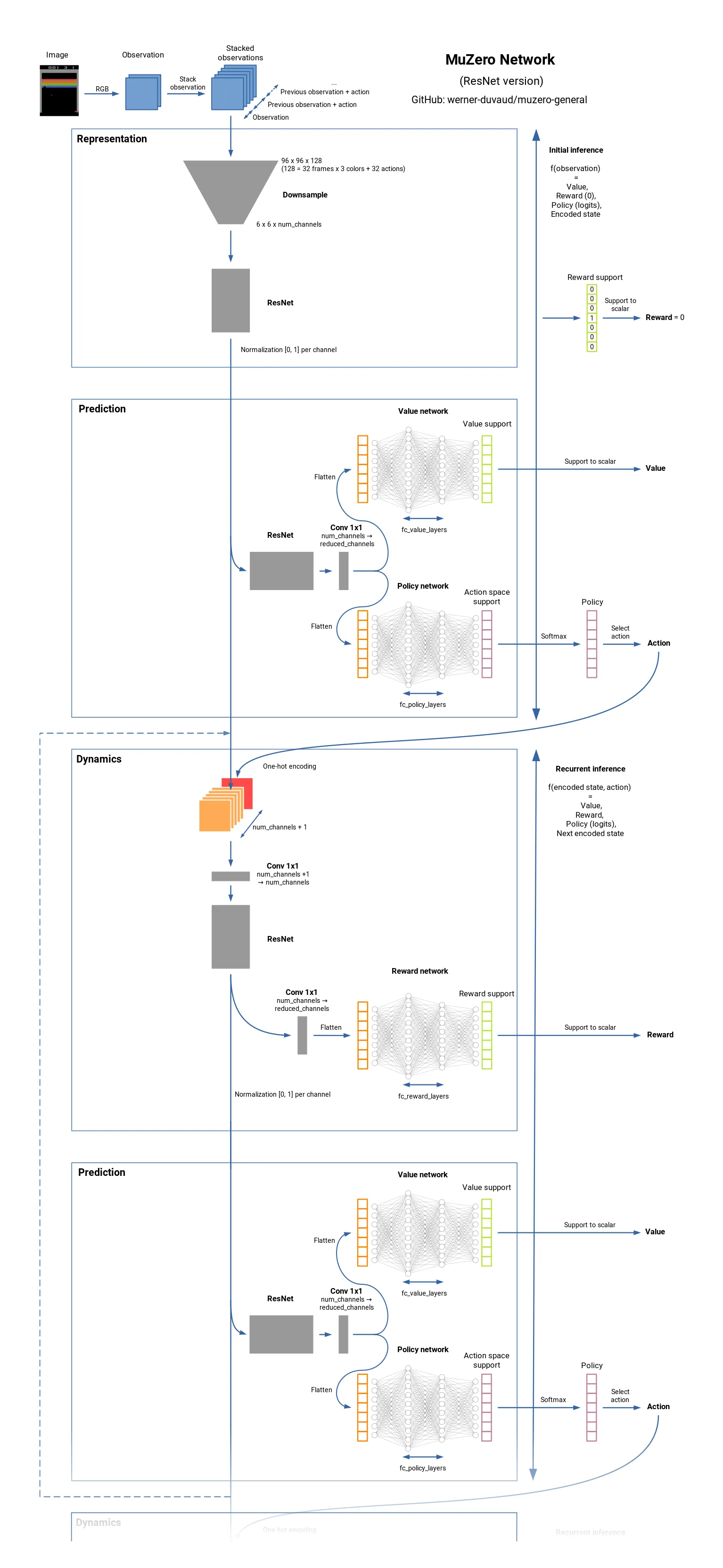
[그림 4.13]에서 확인할 수 있듯이, MuZero는 표현 함수, 동역학 함수, 예측 함수 세 가지의 주요한 함수들로 구성된다.

$s^0=h_{\theta }(o_1,\dots ,o_t)$

$r^k,s^k=g_{\theta }(s^{k-1},a^k)$

$p^k,v^k=f_{\theta }(s^k)$

$\text{[수식 4.9] MuZero의 함수 정의}$

표현 함수(Representation Function)$h_{\theta }$는 관측 이력$(o_1,\dots ,o_t)$을 내부 상태$s^0$로 변환한다.
동역학 함수(Dynamics Function)$g_{\theta }$는 내부 상태$s^{k-1}$와 행동$a^k$를 받아 다음 상태$s^k$와 보상$r^k$를 예측한다.
예측 함수(Prediction Function)$f_{\theta }$는 내부 상태$s^k$에서 정책$p^k$와 가치$v^k$를 출력한다 [29].

학습 과정에서 MuZero는 세 가지 손실을 동시에 최적화한다 [17]. 정책 손실은 MCTS에서 생성된 개선된 정책과 신경망 정책 간의 차이를, 가치 손실은 실제 게임 결과와 가치 예측 간의 차이를, 보상 손실은 실제 보상과 동역학 함수의 보상 예측 간의 차이를 최소화한다.

MuZero의 핵심을 살펴보면, 추상적 상태 표현에서는 실제 환경 상태가 아닌 계획에 유용한 내부 표현을 학습하고, 통합 학습에서는 MCTS 시뮬레이션과 신경망 학습을 동시에 수행한다. 부분 관측 대응에서는 관측 이력을 통해 숨겨진 정보를 추론한다.

MuZero는 Atari, 체스, 바둑뿐만 아니라 부분 관측 환경에서도 우수한 성능을 보여준다 [17]. 그러나 매우 높은 계산 비용(MCTS 시뮬레이션)과 복잡한 신경망 구조로 인한 구현의 어려움이 있다. 또한 하이퍼파라미터에 매우 민감하고, 연속 행동 공간에서의 적용이 제한적이며, 내부 표현의 해석 불가능성으로 인해 디버깅과 분석이 어렵다는 한계가 있다.

4.2. Model Free#

4.2.1 Value Based#

4.2.1.1. Q-Learning#

4.2.1.1.1. 배경 및 문제 정의#

1980년대 후반, 강화학습 연구에서 가장 큰 도전은 환경 모델을 모르는 상황에서도 최적 정책을 학습하는 것이었다. 기존의 동적 계획법은 전이 확률과 보상 함수가 완전히 알려진 경우에만 적용 가능했기 때문에, 실제 환경에서는 사용하기 어려웠다. Christopher Watkins는 이러한 한계를 극복하기 위해 경험을 통해 학습하는 model-free 알고리즘인 Q-learning을 개발했다 [32]. Q-Learning은 model-free 강화학습의 기초적이고 핵심적인 알고리즘으로, 후속 연구들의 이론적 토대를 제공하므로 상세히 다룬다 [2].

4.2.1.1.2. 알고리즘 설계#

Q-learning의 아이디어는 환경 모델 없이도 최적 정책을 학습할 수 있다는 것이다. 기존 동적 프로그래밍이 전이 확률 P(s’|s,a)와 보상 함수 R(s,a)를 필요로 했다면, Q-learning은 실제 경험 (s, a, r, s’)만으로 Q-value를 업데이트한다 [2]. Q-learning의 핵심은 행동-가치 함수$Q(s,a)$를 직접 학습하는 것이다. 이는 상태$s$에서 행동$a$를 취한 후 최적 정책을 따를 때의 기대 누적 보상을 나타낸다.

$Q^{\ast }(s,a)=R(s,a)+\gamma {\sum }_{s^{\prime }}P(s^{\prime }|s,a){\max }_{a^{\prime }}{Q}^{\ast }(s^{\prime },a^{\prime })$

$\text{[수식 4.10] 벨만 최적 방정식}$

[수식 4.10]은 Q-value를 계산하는 수식으로 현재 즉시 제공되는 보상과 할인 인자가 곱해진 미래 가치 기댓값과의 합을 의미한다.

Q-learning의 업데이트 규칙은 시간차 학습(Temporal Difference Learning)을 기반으로 한다.

$Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma {\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })-Q(s,a)\right]$

$\text{[수식 4.11] Q-Learning 업데이트 규칙}$

[수식 4.11]에서는$\alpha$는 학습률,$r$은 관찰된 즉시 보상,$\gamma$는 할인 인자이다. 대괄호 안의 항은 시간차 오차(TD Error)로, 현재 추정값과 실제 경험 사이의 차이를 나타낸다 [2].

$\text{[그림 4.14] Q-Learning 의사코드}$

Q-learning의 중요한 특징 중 하나는 off-policy 학습이 가능하다는 점이다 [2]. 이는 학습하려는 목표 정책(target policy)과 실제 행동을 생성하는 행동 정책(behavior policy)이 다를 수 있음을 의미한다. 구체적으로, Q-learning은$ϵ$-greedy와 같은 탐험적 정책을 사용해 데이터를 수집하면서도, greedy 정책에 대한 Q-value를 학습할 수 있다.

4.2.1.1.3. 수렴성 조건#

• 학습률(Learning rate,${\alpha }_n$) 조건

  • 상태-행동 쌍에 대한 학습률의 총합은 무한대로 발산:${\sum }_{i=1}^{\infty }{\alpha }_{n^i(x,a)}=\infty$
  • 학습률 제곱의 총합은 유한한 값으로 수렴:${\sum }_{i=1}^{\infty }[{\alpha }_{n^i(x,a)}{]}^2<\infty$
  • 실용적 학습률 설정:${\alpha }_t=\frac{1}{t}$,${\alpha }_t=\frac{1}{\sqrt{t}}$, 또는 상수 학습률

• 충분한 탐험: 모든 상태에서 모든 가능한 행동을 무한히 반복적으로 경험해야 함

• 이산적 Q-value 표현: Q-value는 개별적인 상태-행동 쌍에 대해 테이블 형태(look-up table)로 표현

• MDP 조건: 학습 환경은 마르코프 결정 과정이어야 함

• 유계성: 에이전트가 받는 모든 보상은 항상 유계한 값이어야 함

이러한 조건 하에서 Q-learning은 확률 1로 최적 Q-function로 수렴한다 [2].

4.2.1.1.4. 탐험 전략#

• ε-greedy 정책: 가장 일반적인 탐험 방법으로, 확률 ε로 무작위 행동을, (1-ε)로 탐욕적 행동을 선택

$$ \pi(a|s) = \begin{cases} 1-\epsilon + \frac{\epsilon}{|A|} & \text{if } a = \arg\max_{a'} Q(s,a') \\ \frac{\epsilon}{|A|} & \text{otherwise} \end{cases} $$

• Boltzmann 탐험: temperature($\tau$)를 사용한 소프트맥스 분포

$\pi (a|s)=\frac{e^{Q(s,a)/\tau }}{{\sum }_{a^{\prime }}{e}^{Q(s,a^{\prime })/\tau }}$

• Upper Confidence Bound (UCB): 불확실성을 고려한 낙관적 탐험으로, 방문 횟수가 적은 행동에 대해 보너스를 제공

4.2.1.1.5. 한계#

• 확장성 문제: 상태 공간과 행동 공간이 클 경우 Q-table의 크기가 기하급수적으로 증가하여 메모리와 계산 시간 측면에서 실용적이지 않음

• 연속 공간의 한계: 연속적인 상태나 행동 공간에서는 Q-table 표현 자체가 불가능하여 함수 근사가 필수적 [4-1]

• 샘플 효율성: 모든 상태-행동 쌍을 충분히 탐험해야 하므로 샘플 효율성이 낮음

• 수렴 속도 문제: 이론적으로는 수렴이 보장되지만, 큰 상태 공간에서는 실용적인 시간 내에 수렴하지 않을 수 있음

4.2.1.1.6. 학문적 의의#

Q-learning은 강화학습 분야의 기초 알고리즘으로서 이후 수십 년간 연구 발전에 지대한 영향을 미쳤다. 이 알고리즘이 제시한 핵심 아이디어들은 현대 강화학습의 근간을 이루고 있으며, 다양한 방향으로 확장되고 발전되었다 [4-1] [32].

4.2.1.2. Deep Q-Network#

4.2.1.2.1. 배경 및 문제 정의#

2010년대 초, 강화학습은 여전히 간단한 tabular 환경이나 저차원 상태 공간에 제한되어 있었다 [12], [25]. 컴퓨터 비전과 자연어 처리에서 딥러닝이 우수한 성과를 보이고 있었지만, 강화학습과의 결합은 여러 기술적 도전으로 인해 성공하지 못하고 있었다. 기존 Q-learning의 확장성 문제와 일반화 능력 부족 등의 한계가 존재했다. DeepMind의 연구팀은 이러한 한계를 극복하고 고차원 상태 공간에서 직접 학습할 수 있는 알고리즘을 개발했다 [4], [4-1]. DQN은 딥러닝과 강화학습을 성공적으로 결합한 첫 번째 사례로서 후속 연구들의 출발점이 되므로 상세히 다룬다.

4.2.1.2.2. 알고리즘 설계#

DQN의 핵심 아이디어는 Q-table을 깊은 신경망으로 대체하여 함수 근사를 통해 Q-value를 학습하는 것이다. 이는 다음과 같이 표현된다:

$Q(s,a;\theta )\approx Q^{\ast }(s,a)$

$\text{[수식 4.12] DQN의 함수 근사}$

[수식 4.12]에서$\theta$는 신경망의 파라미터이다. 이를 통해 연속적이거나 매우 큰 상태 공간에서도 일반화가 가능해진다.

DQN은 시간차 학습의 아이디어를 신경망 학습에 적용한다. 각 시간 단계에서의 손실 함수는 다음과 같이 정의된다:

$L(\theta )={\mathbb{E}}_{(s,a,r,s^{\prime })\sim \mathcal{D}}\left[{\left(y-Q(s,a;\theta )\right)}^2\right]$

$\text{[수식 4.13] DQN의 손실 함수}$

[수식 4.13]에서 타겟 값$y$는 다음과 같다:

$y=r+\gamma {\max }_{a^{\prime }}Q(s^{\prime },a^{\prime };{\theta }^{-})$

$\text{[수식 4.14] DQN 타겟값 정의}$

${\theta }^{-}$는 타겟 네트워크의 파라미터이다.

4.2.1.2.3. 주요 기술적 특징#

전통적인 Q-learning에서는 에이전트가 환경과 상호작용하며 얻은 경험을 즉시 학습에 사용하고 버리는 on-policy 방식을 사용했다 [2]. 이러한 방식은 신경망 기반 강화학습에서 심각한 문제를 야기했다. 연속적인 경험들은 높은 상관관계를 가지고 있어 딥러닝의 기본 가정인 독립항등분포(i.i.d.) 조건을 위배하여 신경망 학습을 불안정하게 만들 수 있다. 또한 각 경험을 한 번만 사용하고 버리는 것은 환경과의 상호작용을 통해 얻은 귀중한 학습 데이터를 낭비하는 것이다.

DQN은 경험 리플레이(Experience Replay)를 통해 이러한 문제들을 해결한다 [4]. 에이전트의 모든 경험$(s,a,r,s^{\prime })$를 고정 크기의 순환 버퍼$\mathcal{D}$에 저장하고, 매 학습 단계에서 버퍼로부터 무작위로 미니배치를 선택하여 신경망을 학습시킨다. 이를 통해 각 경험을 여러 번 재사용할 수 있어 샘플 효율성이 향상되고, 무작위 샘플링으로 데이터 간 상관관계를 완화할 수 있다.

신경망 기반 Q-learning의 또 다른 주요 도전은 비정상적 타겟 문제(Non-stationary Target Problem)이다. 기본적인 Q-learning 업데이트에서 타겟 값과 현재 추정값$Q(s,a;\theta )$모두 동일한 파라미터$\theta$를 사용한다. 신경망의 파라미터가 업데이트될 때마다 타겟 값도 함께 변하기 때문에 Q-function의 근사기(approximator)가 어디를 향해 수렴해야 할지 파악하기 어려워진다.

DQN은 이 문제를 해결하기 위해 별도의 타겟 네트워크(Target Network)$Q(s,a;{\theta }^{-})$를 도입했다 [4-1]. 타겟 네트워크는 메인 네트워크와 동일한 구조를 가지지만, 파라미터${\theta }^{-}$는 주기적으로만 업데이트된다. 타겟 네트워크의 파라미터${\theta }^{-}$는 매$C=10,000$스텝마다 메인 네트워크의 파라미터로 복사(${\theta }^{-}\leftarrow \theta$)된다. 이를 통해 일정 기간 동안 타겟 값이 고정되어 학습 목표가 안정화되고, 파라미터 업데이트로 인한 급격한 변화를 방지할 수 있다.

$\text{[그림 4.15] DQN 의사코드}$

4.2.1.2.4. 네트워크 아키텍처 및 구현#

Atari 게임의 고차원 시각적 입력을 처리하기 위해 DQN은 합성곱 신경망(CNN) 아키텍처를 채택했다 [4], [25].

원시 Atari 프레임을 신경망 입력으로 변환하기 위해 여러 단계의 전처리 과정을 거친다. RGB 이미지를 그레이스케일로 변환하여 계산량을 감소시키고, 다운샘플링한다. 연속된 4프레임을 스택하여 시간적 정보와 객체의 움직임 정보를 포함시키고, 픽셀 값을 (0,1) 범위로 정규화한다.

DQN은 학습률 0.00025의 RMSprop 옵티마이저와 할인 인자 0.99를 사용한다. 경험 리플레이 버퍼는 최대 1,000,000개의 경험을 저장하며, 각 학습 단계에서 크기 32의 미니배치를 무작위로 샘플링한다. 타겟 네트워크는 매 10,000 스텝마다 메인 네트워크의 가중치로 업데이트되며, ε-greedy 정책에서 ε값은 1.0에서 시작하여 1,000,000 스텝에 걸쳐 0.1까지 선형적으로 감소한다 [4-1].

4.2.1.2.5. 실험 설정 및 평가#

DQN의 효과를 검증하기 위해 연구팀은 Atari 2600 게임 환경을 선택했다 [4]. 이는 고차원 픽셀 입력을 직접 처리해야 하고, 다양한 장르의 게임을 포함하며, 인간 점수와 비교 가능한 객관적 평가 지표를 제공하기 때문에 이상적인 테스트베드였다.

DQN의 성능 평가는 체계적인 벤치마킹 방법론을 통해 수행되었다. 각 게임에서 30분간 플레이한 인간 전문가의 최고 점수를 인간 기준선으로 설정하고, 완전히 무작위로 행동을 선택하는 정책의 평균 점수를 하한 기준선으로 사용했다. 이 두 기준점을 바탕으로 에이전트의 성능을 정규화된 점수로 평가했다 [4-1], [31].

4.2.1.2.6. 수렴성 및 안정성 분석#

함수 근사를 사용하는 DQN은 tabular Q-learning과 달리 수렴성이 이론적으로 보장되지 않는다 [32]. 이러한 한계는 신경망이 모든 Q-function을 완벽하게 표현할 수 없는 함수 근사 오차, 선형 함수 근사와 달리 비선형 함수 근사의 복잡한 역학 관계, 그리고 자체 추정값을 사용한 타겟 계산으로 인한 부트스트래핑 과정에서의 편향 축적에서 비롯된다.

이론적 한계에도 불구하고 DQN은 실제로 안정적인 학습을 보여주었다. 이는 경험 리플레이의 정규화 효과, 타겟 네트워크의 안정화 역할, 그리고 적절한 네트워크 아키텍처와 하이퍼파라미터의 조합 덕분이다. 이러한 기법들이 함께 작용하여 이론적 수렴 보장이 없음에도 불구하고 실용적으로 안정적인 학습을 가능하게 했다 [4-1].

4.2.1.2.7. 한계#

• Q-value 과대추정: max 연산자가 노이즈가 있는 추정값에 적용될 때 발생하는 통계적 편향으로 인한 체계적인 과대추정 [5]

• 학습 불안정성: 타겟 분포가 계속 변화하는 비정상적 분포 문제와 신경망의 제한된 표현 능력으로 인한 성능 변동

• 샘플 효율성: 대부분의 Atari 게임에서 인간 수준에 도달하기 위해 4천만~5천만 프레임의 경험이 필요 [10], [38]

• 부분관측 환경: 프레임 스택을 사용하더라도 완전한 상태 정보가 없는 부분관측 환경에서는 성능 제한

4.2.1.2.8. 학문적 의의#

DQN은 딥러닝과 강화학습 결합의 성공 사례로서 과대추정 편향 문제를 해결한 Double DQN [5], 네트워크 아키텍처를 개선한 Dueling DQN [6], 경험 리플레이 효율성을 향상시킨 Prioritized Experience Replay, 그리고 여러 기법들을 통합한 Rainbow DQN [7] 등의 연구 방향을 촉발했다 . DQN은 강화학습 분야에서 딥러닝 혁명의 시작점이 되었으며, 현재까지도 많은 연구의 기초가 되고 있다 [9].

4.2.1.3. Double DQN(Double Deep Q-Network)#

기존 DQN에서는 동일한 네트워크가 행동 선택과 Q-value 평가를 모두 담당하여 Q-value이 과대추정되는 문제가 발생했다. 그래서 Double DQN은 행동 선택은 메인 네트워크로, Q-value 평가는 타겟 네트워크로 분리하여 이 문제를 완화한다. 이를 통해 더 정확한 Q-value 추정과 안정적인 학습 성능을 달성했다 [5].

$\text{[그림 4.16] Double DQN 의사코드}$

$Algorithm13$에서 확인할 수 있듯이, Double DQN은 행동 선택과 Q-value 평가를 분리하는 핵심 아이디어를 채택한다. 행동 선택은 메인 네트워크로, Q-value 평가는 타겟 네트워크로 담당하여 과대추정 편향을 완화한다. 이렇게 두 개의 독립적인 네트워크를 사용함으로써 DQN의 과대추정 편향(overestimation bias)을 줄이고, 더 안정적이고 정확한 학습이 가능해진다.

$y=r+\gamma Q(s^{\prime },\arg {\max }_{a^{\prime }}Q(s^{\prime },a^{\prime };\theta );{\theta }^{-})$

$\text{[수식 4.15] Double DQN의 타겟 값 계산}$

[수식 4.15]$y$는 손실 함수 계산에 사용되는 타겟 값, $\theta$는 메인 네트워크의 파라미터, ${\theta }^{-}$는 타겟 네트워크의 파라미터를 의미한다. 기존 DQN의 [수식 4.14]와 달리, 메인 네트워크가 다음 상태에서 최적 행동을 선택하고, $Q(s^{\prime },\cdot ;{\theta }^{-})$로 타겟 네트워크가 해당 행동의 Q-value를 평가한다.

Double DQN은 DQN의 과대추정 편향을 현저히 줄이고, 더 안정적이고 정확한 학습이 가능해진다. 하지만 Double DQN도 과소추정 문제(underestimation bias)가 발생할 수 있으며, 여전히 샘플 효율성이 낮고 탐험 전략에 대한 근본적인 해결책을 제공하지 못한다는 한계가 존재한다.

4.2.1.4. Dueling DQN(Dueling Deep Q-Network)#

Dueling DQN은 기존 DQN의 Q-value 추정 방식을 개선하기 위해 개발되었다. 기존 DQN에서 Q-value를 직접 추정하던 방식과 달리, Q-value를 상태 가치(State Value)와 행동 우위(Action Advantage)로 분해하여 각각을 별도로 학습함으로써 학습 효율성과 안정성을 향상시켰다 [6].

$\text{[그림 4.17] Dueling DQN Network 구조}$

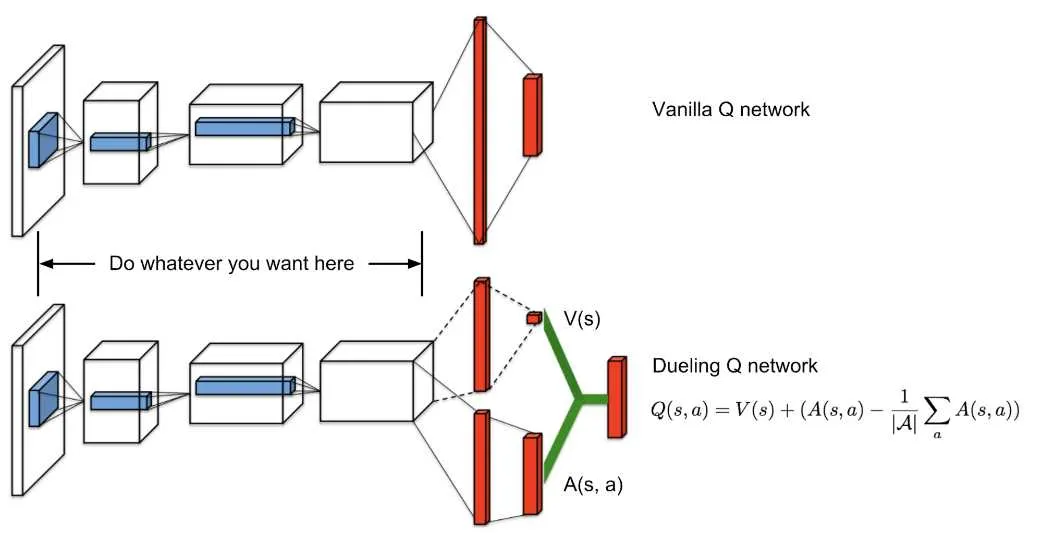
[그림 4.17]에서 확인할 수 있듯이, 기존 Q-network와 달리 Dueling DQN은 공통 특징 추출층 이후 두 개의 분리된 스트림으로 나뉜다. 상단 스트림은 상태 가치 함수$V(s)$를, 하단 스트림은 행동 우위 함수$A(s,a)$를 각각 학습한다.

$Q(s,a;\theta ,\alpha ,\beta )=V(s;\theta ,\beta )+\left(A(s,a;\theta ,\alpha )-\frac{1}{|\mathcal{A}|}{\sum }_{a^{\prime }}A(s,a^{\prime };\theta ,\alpha )\right)$

$\text{[수식 4.16] Dueling DQN의 Q-value 분해 공식}$

[수식 4.16]에서$Q(s,a;\theta ,\alpha ,\beta )$는 최종 Q-value,$V(s;\theta ,\beta )$는 상태 가치 함수(State Value Function), $A(s,a;\theta ,\alpha )$는 행동 우위 함수(Action Advantage Function),$\theta$는 공통 네트워크의 파라미터, $\alpha$는 행동 우위 스트림의 파라미터,$\beta$는 상태 가치 스트림의 파라미터,$|\mathcal{A}|$는 가능한 행동의 개수를 의미한다.

모든 행동의 평균 우위를 빼주는 정규화 항을 통해서 상태 가치와 행동 우위를 명확히 분리하고 식별 가능성(identifiability) 문제를 해결 가능하다. 이러한 구조를 통해 상태의 가치를 독립적으로 학습할 수 있어, 행동 선택이 중요하지 않은 상황에서도 효율적인 학습이 가능하다.

그러나 Dueling DQN은 상태 가치와 행동 우위의 분리 학습을 통해 학습 안정성을 향상시켰지만, 네트워크 구조가 복잡해지고 계산 비용이 증가한다는 단점이 있다. 또한 행동 공간이 매우 클 때 우위 함수 학습의 효과가 제한적일 수 있으며, 정규화항으로 인해 하이퍼파라미터 튜닝이 까다롭다.

4.2.1.5. Rainbow#

Rainbow는 DQN의 여러 개선 기법들을 체계적으로 통합한 강화학습 알고리즘이다 [7]. 개별 기법들이 서로 다른 문제를 해결하기 때문에, 이들을 조합함으로써 단일 기법보다 훨씬 우수한 성능을 달성할 수 있다는 가설을 검증했다.

Rainbow는 상호 보완적인 Double DQN, Dueling DQN, Prioritized Experience Replay, Multi-step Learning, Distributional RL, Noisy Network를 통합했다. 각 기법이 DQN의 서로 다른 한계를 해결하므로, 이들의 조합을 통해 시너지 효과를 창출할 수 있다. 특히 sample efficiency와 final performance를 동시에 향상시키는 것이 주요 목표이다.

Rainbow의 학습은 위 6가지 기법을 순차적으로 적용하는 것이 아니라, 동시에 통합된 형태로 진행된다. Distributional RL을 기반으로 하여 분포적 벨만 연산자를 사용하고, 여기에 Double DQN의 타겟 선택, Dueling 구조의 네트워크, Prioritized replay의 샘플링, Multi-step의 리턴 계산, Noisy network의 탐험이 모두 결합된다.

손실 함수는 distributional DQN을 기반으로 한다.

$\mathcal{L}={\mathbb{E}}_{(s,a,r,s^{\prime })\sim \mathcal{D}}[D_{KL}({\Phi }_z{\hat{T}}^{(n)}{Z}_{\bar{\theta }}(s^{\prime },a^{\ast })||Z_{\theta }(s,a))]$

$\text{[수식 4.17] Rainbow DQN의 분포적 손실 함수}$

[수식 4.17]에서${\Phi }_z$는 분포 투영 연산자이고,${\hat{T}}^{(n)}$은 multi-step distributional Bellman operator이다.

Rainbow는 Atari 게임 환경에서 인간 수준을 크게 뛰어넘는 성능을 보여주며, 특히 data efficiency에서 획기적인 개선을 달성했다. 그러나 Rainbow는 구현 복잡도가 매우 높고 계산 비용이 크게 증가한다는 단점이 있다. 6가지 기법이 결합되면서 하이퍼파라미터 튜닝이 어려워지며, 각 구성 요소 간의 상호작용을 이해하고 디버깅하기 어렵다. 또한 메모리 사용량이 크게 증가하고, 개별 기법의 기여도 분석 없이는 작동 원리 해석이 어렵다는 문제가 존재한다.

4.2.2. Policy Based#

4.2.2.1. REINFORCE#

REINFORCE는 가장 기본적인 정책 기반(policy-based) 강화학습 알고리즘으로, value function을 학습하지 않고 정책을 직접 최적화하는 policy gradient 방법을 사용한다. 연속 행동 공간과 확률적 정책을 자연스럽게 다룰 수 있어 복잡한 제어 문제에 적용 가능하다 [18].

$\text{[그림 4.18] REINFORCE 정책 경사 의사코드}$

$Algorithm16$에서 확인할 수 있듯이, REINFORCE는 전체 에피소드가 완료된 후 실제 리턴 $G_t$를 계산하여 정책을 업데이트한다.

${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{{\pi }_{\theta }}\left[{\sum }_{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)\cdot G_t\right]$

$\text{[수식 4.18] REINFORCE 정책 기울기 공식}$

정책 기울기(policy gradient) 계산은 위 식과 같이 계산되며, 여기서${\nabla }_{\theta }J(\theta )$는 정책 파라미터$\theta$에 대한 목적 함수의 gradient, ${\pi }_{\theta }(a_t|s_t)$는 파라미터$\theta$로 표현된 정책 함수, $G_t$는 시점 t부터의 누적 할인 보상(return),${\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)$는 log 정책의 gradient(score function)를 의미한다.

REINFORCE는 log 정책의 gradient와 실제 받은 보상을 곱하여 좋은 행동의 확률은 높이고 나쁜 행동의 확률은 낮추는 방식으로 작동한다. 각 에피소드에서 수집된 경험을 통해$G_t$를 계산하고, 이를 기반으로 정책 파라미터를 기대 누적 보상을 최대화하는 방향으로 업데이트한다. 그러나 높은 분산 문제와 느린 수렴 속도라는 한계가 있다. Monte Carlo 방법으로 인한 샘플 효율성이 낮고, baseline 없이는 학습이 불안정할 수 있다.

4.2.2.2. TRPO#

TRPO(Trust Region Policy Optimization) 는 기존 policy gradient 방법들의 학습 불안정성 문제를 해결하기 위해 개발되었다. 정책 업데이트 시 과도한 변화로 인한 성능 붕괴를 방지하고자 trust region 개념을 도입하여 안전한 정책 개선을 보장한다 [19].

$\text{[그림 4.19] TRPO 의사코드}$

Algorithm 17에서 확인할 수 있듯이, TRPO는 각 반복에서 현재 정책으로 궤적을 수집하고, GAE(Generalized Advantage Estimation)를 통해 어드밴티지 함수를 추정한다.

${\hat{A}}_t={\delta }_t+(\gamma \lambda ){\delta }_{t+1}+(\gamma \lambda {)}^2{\delta }_{t+2}+\cdots$

$\text{[수식 4.18] GAE를 통한 어드밴티지 추정}$

${\delta }_t=r_t+\gamma V_{\varphi }(s_{t+1})-V_{\varphi }(s_t)$

$\text{[수식 4.19] Temporal Difference Error}$

핵심 최적화 과정은 다음과 같은 제약 최적화 문제를 해결하는 것이다:

${\max }_{{\theta }_{new}}\mathbb{E}\left[\frac{{\pi }_{{\theta }_{new}}(a|s)}{{\pi }_{\theta }(a|s)}\hat{A}(s,a)\right]$

$\text{[수식 4.20] TRPO 대리 목적 함수}$

$\text{subject to }\mathbb{E}[D_{KL}({\pi }_{\theta }(\cdot |s)\Vert {\pi }_{{\theta }_{new}}(\cdot |s))]\le \delta$

$\text{[수식 4.21] TRPO의 신뢰 영역 제약}$

목적 함수에서 중요도 비율은 새로운 정책과 기존 정책 간의 확률 비율을 나타내며, 어드밴티지 함수와 곱해져 정책 개선 방향을 결정한다. 제약 조건의 δ는 trust region의 크기를 제어하는 하이퍼파라미터이다.

TRPO는 conjugate gradient 방법을 사용하여 KL divergence 제약 하에서 surrogate objective를 최대화하는 정책 업데이트를 수행한다. 동시에 가치 함수는 다음과 같이 업데이트된다.

$\varphi \leftarrow \arg {\min }_{\varphi }\mathbb{E}[(V_{\varphi }(s)-V^{target}{)}^2]$

$\text{[수식 4.22] 가치 함수 업데이트}$

TRPO는 단조적 성능 개선을 이론적으로 보장하며 안정적인 정책 학습을 제공하지만, conjugate gradient와 line search를 포함한 복잡한 최적화 과정으로 인해 계산 비용이 높고 구현이 복잡하다는 한계를 갖는다.

4.2.2.3. PPO(Proximal Policy Optimization)#

4.2.2.3.1. 배경 및 문제 정의#

2017년, 강화학습 분야는 DQN의 성공으로 가치 기반 방법론이 주목받았으나, 여전히 중요한 한계들이 존재하였다. DQN은 이산적인 행동 공간에만 적용 가능하였고, 연속적인 제어 문제나 확률적 정책이 필요한 상황에서는 사용할 수 없었다.

이러한 문제를 해결하기 위해 정책을 직접 학습하는 정책 경사 방법(Policy Gradient Methods)이 연구되었다. REINFORCE [18]는 몬테카를로 방법을 사용해 정책을 직접 최적화하였지만 높은 분산으로 인한 학습 불안정성 문제가 있었다. Actor-Critic 방법들(A3C [20] 등)은 가치 함수를 baseline으로 사용해 분산을 줄였으나, 여전히 스텝 크기 결정과 학습 안정성에서 어려움을 겪었다.

Trust Region Policy Optimization(TRPO) [19]은 정책 업데이트 시 KL divergence 제약을 통해 안전한 학습을 보장하였지만, 구현이 복잡하고 계산 비용이 높다는 한계가 있었다. OpenAI의 연구팀은 이러한 문제들을 해결하고자 TRPO의 이론적 장점을 유지하면서도 구현이 간단하고 계산 효율적인 PPO [3]를 개발했다. PPO는 현대 강화학습에서 가장 널리 사용되는 정책 기반 알고리즘 중 하나로 자리잡았으며, 실무적 적용성과 이론적 견고함을 동시에 갖춘 중요한 알고리즘이므로 상세히 다룬다.

4.2.2.3.2. 알고리즘 설계#

정책 경사법의 기본 원리

정책 경사법의 핵심 아이디어는 정책 파라미터 θ를 직접 최적화하여 기대 누적 보상을 최대화하는 것이다.

$J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[R(\tau )]$

$\text{[수식 4.23] 정책 최적화 목적 함수}$

여기서 τ는 궤적(trajectory), R(τ)는 누적 보상이다. Policy Gradient Theorem에 따르면, 목적 함수의 gradient는 다음과 같다.

${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[{\sum }_{t=0}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)A^{{\pi }_{\theta }}(s_t,a_t)\right]$

$\text{[수식 4.24] Policy Gradient Theorem}$

여기서 [수식 4.24]의 어드밴티지 함수는 해당 상태에서 특정 행동이 평균적인 행동보다 얼마나 좋은지를 나타낸다.

Surrogate Objective

PPO의 핵심은 대리 목적 함수(Surrogate Objective)를 사용하는 것이다. 기존 정책에서 새로운 정책으로 업데이트할 때, importance sampling을 사용하여 다음과 같이 표현할 수 있다.

$L^{CPI}(\theta )={\mathbb{E}}_t\left[\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{{\theta }_{old}}(a_t|s_t)}{A}_t\right]={\mathbb{E}}_t[r_t(\theta )A_t]$

$\text{[수식 4.25] Conservative Policy Iteration 목적 함수}$

$r_t(\theta )=\frac{{\pi }_{\theta }(a_t|s_t)}{{\pi }_{{\theta }_{old}}(a_t|s_t)}$

$\text{[수식 4.26] 정책 간 확률 비율}$

여기서 수식 [4.26]은 확률 비율(probability ratio)이다.

Clipped Surrogate Objective

PPO의 주목할 만한 혁신은 클리핑된 대리 목적 함수이다. 확률 비율이 너무 크게 변하는 것을 방지하기 위해 다음과 같이 클리핑을 적용한다.

$L^{CLIP}(\theta )={\mathbb{E}}_t[\min (r_t(\theta )A_t,\text{clip}(r_t(\theta ),1-ϵ,1+ϵ)A_t)]$

$\text{[수식 4.27] PPO 클리핑된 대리 목적 함수}$

$\text{clip}(x,a,b)=\max (a,\min (x,b))$

$\text{[수식 4.28] 클리핑 함수 정의}$

여기서 [수식 4.28]과 같이 정의된 클리핑 함수에서 ε은 클리핑 범위를 나타내는 하이퍼파라미터(일반적으로 0.1~0.3)이다.

전체 손실 함수

PPO의 전체 손실 함수는 정책 손실, 가치 함수 손실, 엔트로피 보너스를 결합한다.

$L(\theta ,\varphi )=L^{CLIP}(\theta )+c_1{L}^V(\varphi )-c_2\mathbb{H}[{\pi }_{\theta }(\cdot |s)]$

$\text{[수식 4.29] PPO 전체 손실 함수}$

$L^V(\varphi )=(V_{\varphi }(s)-V^{target}{)}^2$

$\text{[수식 4.30] 가치 함수 손실}$

여기서 [수식 4.30]은 가치 함수 손실이고, 엔트로피 보너스는 탐험을 장려하며, c₁, c₂는 가중치 계수(일반적으로 c₁ = 0.5, c₂ = 0.01)이다.

4.2.2.3.3. 구현 및 학습 과정#

Actor-Critic 아키텍처

PPO는 일반적으로 Actor-Critic 구조를 사용한다. Actor는 정책을 출력하는 신경망이고, Critic은 상태 가치 함수를 추정하는 신경망이다. 연속 행동 공간에서는 Actor가 가우시안 분포의 평균과 표준편차를 출력하고, 이산 행동 공간에서는 각 행동의 확률을 출력한다.

Generalized Advantage Estimation (GAE)

어드밴티지 함수의 정확한 추정을 위해 GAE를 사용한다.

$A_t^{GAE(\gamma ,\lambda )}={\sum }_{l=0}^{\infty }(\gamma \lambda {)}^l{\delta }_{t+l}^V$

$\text{[수식 4.31] Generalized Advantage Estimation}$

[수식 4.31]에서 λ는 편향-분산 트레이드오프를 조절하는 하이퍼파라미터이며,${\delta }_t^V$는 [수식 4.19]의 TD Error이다.

학습 알고리즘

$\text{[그림 4.20] PPO 학습 의사코드}$

PPO 학습 과정은 Algorithm 5와 같이 구성된다. 먼저 정책 네트워크와 가치 함수를 초기화하고, 클리핑 범위 ε, 에포크 수 K, 타임스텝 T, 할인율 γ, GAE 파라미터 λ 등의 하이퍼파라미터를 설정한다.

각 반복에서는 먼저 데이터 수집 단계를 수행한다. 환경에서 상태를 관찰하고, 현재 정책에서 행동을 샘플링하여 실행한 뒤, 보상과 다음 상태를 수집한다.

다음으로 어드밴티지 계산 단계에서는 각 궤적에 대해 [수식 4.31]와 다음 수식의 리턴을 구한다.

$R_t=A_t+V_{\varphi }(s_t)$

$\text{[수식 4.32] 타겟 리턴 계산}$

정책 업데이트 단계에서는 K번의 에포크에 걸쳐 [수식 4.26]의 확률 비율을 계산하고, [수식 4.27]의 클리핑된 대리 목적 함수를 이용하여 정책을 업데이트한다. 마지막으로 가치 함수 업데이트 단계에서는 다음 수식의 가치 손실을 계산하여 가치 함수를 업데이트한다.

$L^V(\varphi )=(V_{\varphi }(s_t)-R_t{)}^2$

$\text{[수식 4.33] 실제 가치 함수 업데이트 손실}$

PPO의 클리핑 메커니즘은 정책 성능의 단조 개선을 이론적으로 보장한다. 클리핑된 목적 함수는 실제 목적 함수의 하한을 제공하며, 이를 최적화하면 최악의 경우에도 성능이 악화되지 않는다. PPO의 클리핑은 암묵적으로 신뢰 영역 제약과 유사한 효과를 가지며, KL divergence 제약을 명시적으로 사용하는 TRPO와 달리 확률 비율 클리핑을 통해 유사한 안전성을 달성한다. PPO의 변형으로는 클리핑 대신 KL divergence 페널티를 사용하는 PPO-Penalty가 있으며, 이는 다음과 같이 표현된다.

$L^{KLPEN}(\theta )={\mathbb{E}}_t[r_t(\theta )A_t-\beta \text{KL}[{\pi }_{{\theta }_{old}},{\pi }_{\theta }]]$

$\text{[수식 4.34] PPO-Penalty 목적 함수}$

또한 KL divergence가 목표 값을 벗어나면 β를 동적으로 조정하여 제약을 유지하는 적응적 KL 계수 방법도 제안되었다.

4.2.2.3.4. 한계#

PPO의 성공에도 불구하고 여러 근본적인 한계와 도전 과제들이 존재한다. 가장 주요한 문제는 여전히 높은 샘플 복잡도이다. 복잡한 환경에서 인간 수준의 성능에 도달하기 위해서는 상당한 양의 환경 상호작용이 필요하며, 이는 실제 물리적 시스템에서의 적용을 제약하는 요인이 된다. 하이퍼파라미터에 대한 민감성 또한 실용적 관점에서 중요한 문제이다. 클리핑 범위 ε, 학습률, 배치 크기 등의 설정이 최종 성능에 상당한 영향을 미치며, 새로운 환경에 적용할 때마다 광범위한 하이퍼파라미터 탐색이 필요할 수 있다. 부분관측 환경에서의 한계도 주목할 만하다. POMDP 설정에서는 현재 상태만으로는 최적 행동을 결정할 수 없어 메모리 메커니즘이 필수적이지만, 순환 신경망과 같은 메모리 구조를 통합할 경우 학습의 복잡도가 크게 증가한다. 또한 다중 에이전트 환경에서는 다른 에이전트들의 정책 변화로 인한 비정상성 문제가 추가적으로 발생할 수 있다.

4.2.2.3.5. 학문적 의의#

PPO는 강화학습 분야에서 정책 기반 방법론의 실용화에 큰 기여를 했다. TRPO [19]의 이론적 견고함을 유지하면서도 구현의 복잡성을 크게 줄여, 강화학습의 실무 적용을 촉진했다 [3].

현재 OpenAI GPT 시리즈의 인간 피드백 강화학습(RLHF)을 비롯해 다양한 대규모 AI 시스템에서 PPO가 핵심 알고리즘으로 사용되고 있으며, 강화학습의 산업적 응용 확산에 중요한 역할을 하고 있다.

4.2.3. Actor-Critic#

4.2.3.1. A2C/A3C#

A2C(Advantage Actor-Critic) 와 A3C(Asynchronous Advantage Actor-Critic) 는 Actor-Critic 구조를 기반으로 정책 기반 강화학습의 높은 분산 문제를 해결하기 위해 개발되었다. 기존 REINFORCE 알고리즘의 샘플 효율성과 학습 안정성 한계를 극복하고자 advantage function을 도입하여 정책 업데이트의 분산을 크게 감소시켰다 [20].

$\text{[그림 4.21] A2C 알고리즘 의사코드}$

Algorithm 19에서 제시된 바와 같이, A2C는 Actor 네트워크$\pi (a|s;\theta )$와 Critic 네트워크$V(s;\varphi )$를 동시에 학습한다. 각 타임스텝에서 Actor는 현재 정책에 따라 행동을 샘플링하고, 환경으로부터 보상과 다음 상태를 관찰한다.

가치 추정 및 Advantage 계산에서 Critic은 다음 수식의 TD target을 계산한다.

$V_{target}=r_{t+1}+\gamma V(s_{t+1};\varphi )$

$\text{[수식 4.35] TD Target 계산}$

이후 advantage function은 다음과 같이 정의된다.

$A_t=V_{target}-V(s_t;\varphi )$

$\text{[수식 4.36] Advantage Function 정의}$

[수식 4.36]는 현재 행동이 해당 상태의 평균적 가치보다 얼마나 우수한지를 측정한다.

동시 업데이트 과정에서 Critic은 다음 수식의 TD error 제곱손실을 최소화하여 상태 가치 함수를 학습한다.

${\nabla }_{\varphi }(V_{target}-V(s_t;\varphi ){)}^2$

$\text{[수식 4.37] Critic 손실 함수}$

Actor는 다음 수식의 advantage로 가중된 정책 기울기로 정책을 개선한다.

$A_t{\nabla }_{\theta }\ln \pi (a_t|s_t;\theta )$

$\text{[수식 4.38] Actor 정책 기울기}$

A3C의 확장에서는 여러 워커가 독립적인 환경에서 비동기적으로 학습을 수행하여 전역 네트워크를 업데이트한다 [20]. 이를 통해 샘플 효율성과 exploration이 향상되며 학습 속도가 가속화된다. 그러나 비동기 업데이트로 인한 구현 복잡성과 워커 간 동기화 문제, 높은 계산 자원 요구량이라는 한계가 존재한다.

4.2.3.2. DDPG#

DDPG(Deep Deterministic Policy Gradient) 는 연속 행동 공간에서의 제어 문제를 해결하기 위해 개발된 Actor-Critic 알고리즘이다 [21]. 기존 DQN[4]이 이산 행동 공간에 제한되어 있던 한계를 극복하고, 결정론적 정책을 통해 연속적인 행동을 직접 출력할 수 있도록 설계되었다.

$\text{[그림 4.22] DDPG 알고리즘 의사코드}$

$Algorithm20$에서 확인할 수 있듯이, Actor는 결정론적 정책${\mu }_{{\theta }_{\mu }}(s)$를 학습하여 주어진 상태에서 최적의 행동을 출력하고, Critic은 Q-function$Q(s,a;{\theta }_Q)$를 학습하여 상태-행동 쌍의 가치를 평가한다.

정책 업데이트는 다음 수식의 정책 기울기를 통해 수행된다:

${\nabla }_{{\theta }^{\mu }}J\approx \frac{1}{N}{\sum }_i{\nabla }_{a}Q(s,a|{\theta }^Q){|}_{a=\mu (s_i|{\theta }^{\mu })}{\nabla }_{{\theta }^{\mu }}\mu (s|{\theta }^{\mu }){|}_{s_i}$

$\text{[수식 4.39] DDPG 정책 기울기 (표본 기반)}$

$={\mathbb{E}}_{s\sim {\rho }^{\beta }}\left[{\nabla }_{a}Q(s,a;{\theta }_Q){|}_{a={\mu }_{{\theta }_{\mu }}(s)}{\nabla }_{{\theta }_{\mu }}{\mu }_{{\theta }_{\mu }}(s)\right]$

$\text{[수식 4.40] DDPG 정책 기울기 (기댓값 형태)}$

Critic 업데이트는 DQN과 유사하게 temporal difference error를 최소화하는 방식으로 진행된다.

$L=\frac{1}{N}{\sum }_i(y_i-Q(s_i,a_i|{\theta }^Q){)}^2$

$\text{[수식 4.41] Critic 손실 함수}$

$y_i=r_i+\gamma Q^{\prime }(s_{i+1},{\mu }^{\prime }(s_{i+1}|{\theta }^{{\mu }^{\prime }})|{\theta }^{Q^{\prime }})$

$\text{[수식 4.42] DDPG TD Target 계산}$

여기서 [수식 4.42]의 타겟 네트워크 매개변수는 경험 리플레이 버퍼에서 샘플링된 전이에 대해 behavior policy에 의한 상태 분포를 반영한다.

DDPG는 경험 리플레이를 통해 샘플 효율성을 높이고, 타겟 네트워크를 다음 수식의 soft update 방식으로 점진적으로 업데이트하여 학습을 안정화한다.

${\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime }$

$\text{[수식 4.43] 타겟 네트워크 Soft Update}$

또한 연속 행동 공간을 자연스럽게 처리하고 높은 샘플 효율성과 안정적인 학습을 제공한다. 그러나 하이퍼파라미터에 민감하고 탐험 전략이 제한적이며, overestimation bias 문제가 발생할 수 있는 한계가 존재한다.

4.2.3.3. SAC#

SAC(Soft Actor-Critic) 는 기존 강화학습의 exploitation에 치중된 문제를 해결하기 위해 최대 엔트로피 강화학습(maximum entropy reinforcement learning) 프레임워크를 도입한 off-policy Actor-Critic 알고리즘이다 [22]. 보상 최대화와 함께 정책의 엔트로피를 동시에 최대화하여 exploration과 exploitation의 균형을 자동으로 조절한다.

$\text{[그림 4.23] SAC 의사코드}$

Algorithm 21에서 확인할 수 있듯이, SAC는 정책${\pi }_{\varphi }$와 두 개의 Q-function$Q_{{\theta }_1},Q_{{\theta }_2}$를 동시에 학습하며, 확률적 정책을 사용하여 overestimation bias를 완화한다.

최대 엔트로피 목적 함수는 다음과 같이 정의된다.

$J(\pi )={\mathbb{E}}_{\tau \sim \pi }\left[{\sum }_{t=0}^{T}r(s_t,a_t)+\alpha \mathcal{H}(\pi (\cdot |s_t))\right]$

$\text{[수식 4.44] SAC 최대 엔트로피 목적 함수}$

$\mathcal{H}(\pi (\cdot |s))=-{\mathbb{E}}_{a\sim \pi (\cdot |s)}[\log \pi (a|s)]$

$\text{[수식 4.45] 정책 엔트로피 정의}$

[수식 4.45]에서 α는 엔트로피 가중치(temperature parameter)를 의미한다.

SAC의 정책 업데이트는 정책 기울기 방법을 통해 수행된다.

${\nabla }_{\theta }J({\pi }_{\theta })={\mathbb{E}}_{s,a\sim \mathcal{D}}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)(Q_{\varphi }(s_t,a_t)-\alpha \log {\pi }_{\theta }(a_t|s_t))\right]$

$\text{[수식 4.46] SAC 정책 기울기}$

Critic 업데이트는 두 개의 Q-function을 사용하여 다음과 같이 진행된다.

$L(\varphi )={\mathbb{E}}_{(s,a,r,s^{\prime })\sim \mathcal{D}}\left[(Q_{\varphi }(s,a)-y{)}^2\right]$

$\text{[수식 4.47] SAC Critic 손실 함수}$

$y=r+\gamma {\mathbb{E}}_{a^{\prime }\sim {\pi }_{\theta }(\cdot |s^{\prime })}[Q_{\bar{\varphi }}(s^{\prime },a^{\prime })-\alpha \log {\pi }_{\theta }(a^{\prime }|s^{\prime })]$

$\text{[수식 4.48] SAC TD Target 계산}$

여기서 [수식 4.47]의 Critic Q-function과 [수식 4.48]의 타겟 Q-function은 확률적 정책과 함께 엔트로피 정규화를 포함한 타겟 계산을 수행한다.

SAC의 핵심 혁신은 정책의 엔트로피를 보상에 직접 포함시켜 높은 불확실성을 유지하면서 exploration을 촉진하는 것이다. 또한 두 개의 Q-function 중 작은 값을 사용하여 overestimation을 방지하고, 자동 엔트로피 조정 기법을 통해 α 값을 동적으로 조절할 수 있다.

SAC는 자동 exploration과 높은 sample efficiency, 안정적인 학습 성능을 제공한다. 그러나 하이퍼파라미터가 많고 계산 비용이 높으며, 엔트로피 가중치 설정이 성능에 큰 영향을 미치는 한계가 존재한다.

4.2.3.4. TD3#

TD3(Twin Delayed Deep Deterministic Policy Gradient)는 DDPG의 overestimation bias와 학습 불안정성 문제를 해결하기 위해 제안된 알고리즘이다 [23]. DDPG가 단일 critic network의 과대추정으로 인해 성능 저하를 겪는 문제를 인식하고, 세 가지 핵심 기법을 통해 더욱 안정적인 학습을 가능하게 했다.

[그림 4.24] TD3 의사코드

$Algorithm22$에서 확인할 수 있듯이, TD3는 Twin Q-networks, Delayed policy update, Target policy smoothing의 세 가지 핵심 메커니즘을 결합한다.

Twin Q-networks를 통해 TD3는 두 개의 독립적인 critic network를 사용하여 overestimation bias를 완화한다. 두 critic의 손실함수는 다음과 같이 정의된다:

$L({\theta }_1,{\theta }_2)={\mathbb{E}}_{(s,a,r,s^{\prime })\sim \mathcal{D}}\left[(Q_{{\theta }_1}(s,a)-y{)}^2+(Q_{{\theta }_2}(s,a)-y{)}^2\right]$

$y=r+\gamma {\min }_{i=1,2}{Q}_{{\theta }_i^{\prime }}(s^{\prime },{\tilde{a}}^{\prime })$

$\text{[수식 4.49] Twin Q-networks의 손실 함수}$

[수식 4.49]에서의 핵심은 두 Q-network 중 최솟값을 선택하여 과대추정을 방지하는 것이다.

Target policy smoothing은 다음과 같이 타겟 정책에 노이즈를 추가하여 함수 근사 오차를 완화한다.

${\tilde{a}}^{\prime }=\text{clip}({\pi }_{{\varphi }^{\prime }}(s^{\prime })+\text{clip}(ϵ,-c,c),a_{low},a_{high})$

$\text{[수식 4.50] Target policy smoothing을 통한 행동 생성}$

[수식 4.50]에서$ϵ\sim \mathcal{N}(0,{\tilde{\sigma }}^2)$는 가우시안 노이즈이며,$c$는 노이즈 clipping 범위를 의미한다.

Delayed policy update는 정책을 critic보다 느린 주기로 업데이트하여 학습 안정성을 확보한다. 정책 기울기는 다음과 같이 계산된다:

${\nabla }_{\varphi }J(\varphi )={\mathbb{E}}_{s\sim \mathcal{D}}\left[{\nabla }_{\varphi }{\pi }_{\varphi }(s){\nabla }_a{Q}_{{\theta }_1}(s,a){|}_{a={\pi }_{\varphi }(s)}\right]$

$\text{[수식 4.51] 지연된 정책 업데이트의 기울기 계산}$

TD3는 DDPG 대비 향상된 안정성과 overestimation bias 완화를 통해 robust한 성능을 제공한다. 하지만 구현 복잡성 증가, 다수의 하이퍼파라미터 조정 필요, 계산 오버헤드 존재, 그리고 여전한 sample efficiency 한계를 갖는다.

5. Comparison and Evaluations#

5.1. 서론#

강화학습 분야의 발전을 정확히 평가하기 위해서는 객관적이고 재현 가능한 성능 지표가 필요하다. 본 논문의 분석에서는 두 가지 주요 벤치마크 환경인 Atari 게임과 MuJoCo 연속 제어 환경에서의 실제 성능 데이터를 바탕으로 주요 강화학습 알고리즘들을 체계적으로 비교한다.

5.2. Atari 환경에서의 성능 비교#

Atari 벤치마크에서는 Human-Normalized Score (HNS)를 사용하여 성능을 평가한다 [4-1]. 이는 다음과 같이 계산된다:

$$HN{S}_{g,i}=\frac{G_{g,i}-G_{g,\text{random}}}{G_{g,\text{human average}}-G_{g,\text{random}}}$$

$\text{[수식 5.1] Human-Normalized Score}$

알고리즘 i의 게임 g에 대한 점수이며, 각기 다른 점수 체계를 가진 게임들의 점수를 정규화함으써 여러 알고리즘들의 성능을 비교할 수 있다.

5.2.1. 주요 알고리즘별 성능#

최근 연구결과에 따르면 Atari 벤치마크에서의 성능은 다음과 같다 [7]:

$\text{[그림 5.1] Rainbow 성능 벤치마크(Median HNS 지표)}$

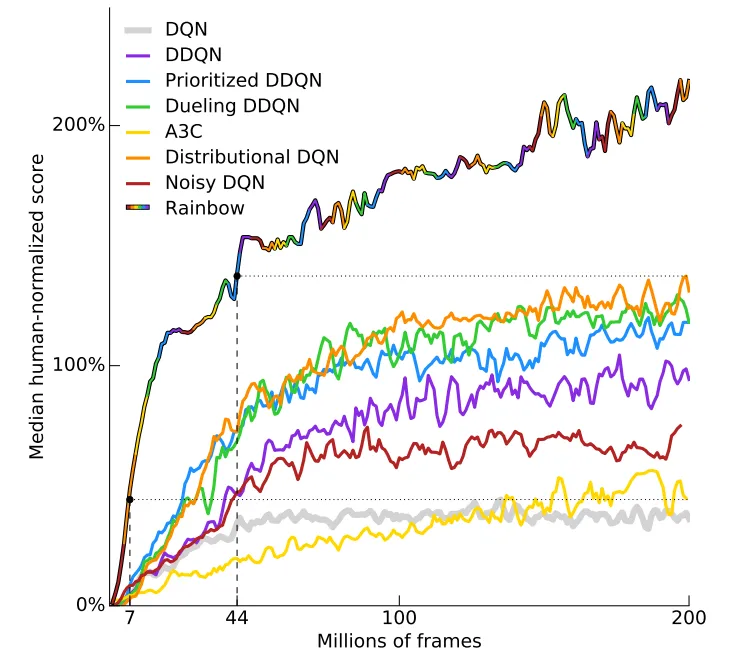
5.2.2. 성능 해석의 문제점#

그러나 기존 평가 기준에는 중요한 한계가 있다. Valeo.ai 연구팀의 분석에 따르면 [31]

DQN 논문 [4-1] 비교 연구의 초보자 수준 인간 성능과 세계 기록 기준 인간 최고 성능 비교 시 많은 차이가 있다는 것이다.

$\text{[그림 5.2] Atari 게임 세계기록 대비 일반 플레이어 성능 비교}$

[//]: # ([Figure 4 추천 위치]: 기존 인간 기준선 vs 세계 기록 기준선 비교 그래프 (Rainbow DQN의 성능이 두 기준에서 어떻게 다르게 평가되는지 시각화))

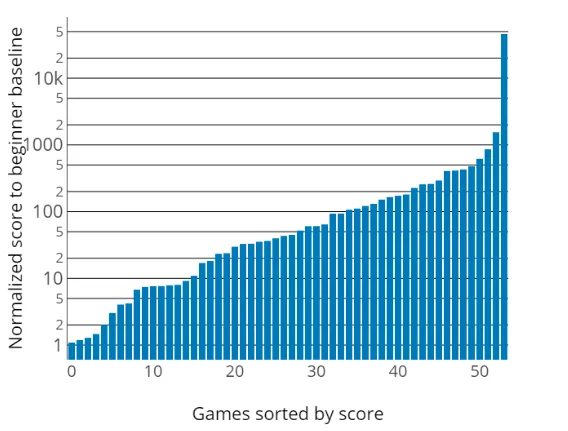
[그림 5.2]에서 특히 주목할 만한 점은 VideoPinball 게임에서 세계 기록이 기존 인간 기준선보다 약 5,050배 높다는 사실이다 [31]. 이는 기존 평가 방식이 실제 인간의 최고 성능을 크게 과소평가했음을 보여준다.

5.2.3. 방법론별 직접 비교 연구#

최근 DQN, PPO, A2C의 직접적인 비교 연구 [24]가 수행되어 방법론 간 차이점을 명확히 보여주었다. 이 연구는 Breakout Atari 게임 환경에서 Stable Baselines3 구현을 사용하여 동일한 조건에서 세 알고리즘을 비교했다.

5.2.3.1. 학습 안정성과 하이퍼파라미터 민감도#

연구 결과 [24]에 따르면 각 알고리즘의 하이퍼파라미터 민감도가 크게 다르다.

DQN이 하이퍼파라미터 변화에 대해 가장 우수한 안정성을 보이는 것은 experience replay buffer와 target network라는 두 가지 핵심 안정화 메커니즘 때문이다. Experience replay buffer는 과거 경험을 저장하고 무작위 샘플링을 통해 학습 데이터의 상관관계를 제거함으한 설정으로써 학습률의 부적절로 인한 부정적 영향을 완화시킨다 [4-1]. 또한 target network의 주기적 업데이트는 Q-value 추정의 안정성을 보장하여 하이퍼파라미터에 대한 알고리즘의 견고성을 높인다 [5].

반면, A2C가 학습률에 극도로 민감한 반응을 보이는 것은 알고리즘의 직접적인 정책 경사법(policy gradient) 업데이트 메커니즘과 관련이 있다. A2C는 별도의 안정화 장치 없이 actor와 critic을 동시에 학습시키므로, 부적절한 학습률은 두 네트워크 간의 학습 속도 불균형을 야기하여 전체 시스템의 불안정성으로 이어진다 [20]. 특히 낮은 학습률에서는 critic의 가치 함수 근사가 충분히 이루어지지 않아 actor에게 부정확한 기울기 정보를 제공하게 된다.

PPO의 중간 정도 안정성은 클리핑 메커니즘의 효과를 반영한다. PPO는 정책 업데이트의 크기를 제한함으로써 급격한 정책 변화를 방지하지만 [3], DQN만큼의 완충 효과를 제공하지는 못한다.

$\text{[그림 5.3] DQN, PPO, A2C의 학습률, 할인 계수에 따른 성능지표}$

[//]: # ([Figure 16 추천 위치]: 학습률별 알고리즘 성능 비교 (DQN, PPO, A2C의 학습률 변화에 따른 성능 곡선을 한 그래프에 표시))

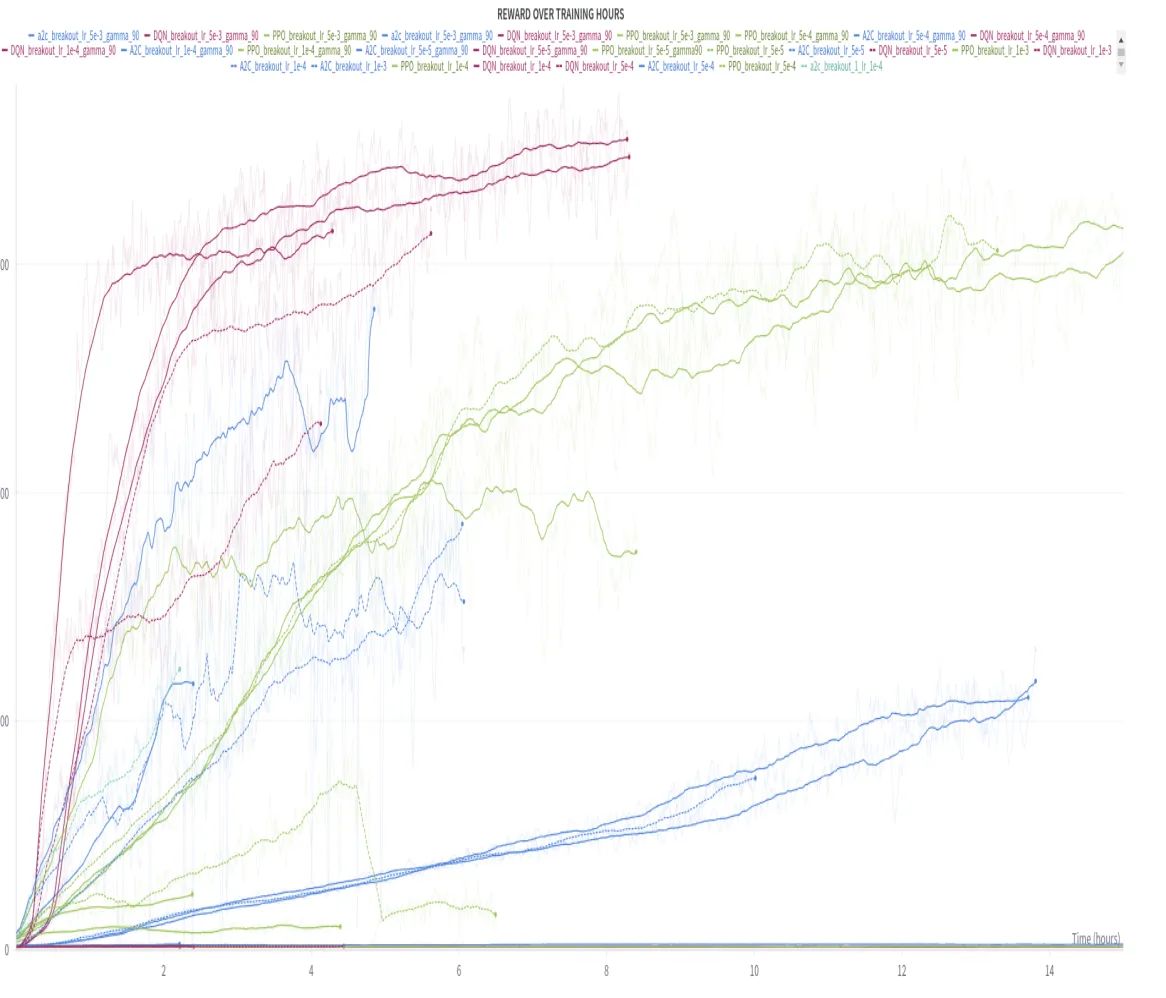
5.2.3.2. 학습 효율성 분석#

프레임 효율성에서 DQN이 가장 우수한 성과를 보이는 것은 off-policy 학습의 본질적 장점에서 기인한다. DQN은 experience replay를 통해 과거 경험을 반복적으로 활용할 수 있어 동일한 환경 상호작용으로부터 더 많은 학습 기회를 얻는다 [4-1]. 이는 sample efficiency 측면에서 상당한 이점을 제공한다.

반대로 PPO와 A2C는 on-policy 알고리즘의 특성상 매번 새로운 데이터를 수집해야 하므로 환경과의 상호작용 횟수가 증가한다 [3] [20]. 특히 PPO는 탐색적 정책으로 인해 더 긴 에피소드를 경험하는 경향이 있어 중간 정도의 효율성을 보인다.

5.2.3.3. 할인 계수의 영향#

할인 계수에 대한 각 알고리즘의 서로 다른 반응은 value-based 방법과 policy-based 방법의 근본적 차이를 반영한다. DQN이 중간 정도의 할인 계수에서 최적 성능을 보이는 것은 높은 할인 계수가 Q-value 추정의 분산을 증가시키고 수렴 속도를 저하시키기 때문이다 [2].

반면 PPO와 A2C가 높은 할인 계수를 선호하는 것은 정책 기반 방법이 장기적 궤적 최적화에 더 적합하기 때문이다 [18]. 이들 알고리즘은 전체 궤적에 대한 정보를 직접 활용하므로 장기 보상을 고려한 전략적 행동 학습에 유리하다.

주목할 점은 앞서 논의한 학습률 민감도와 할인 계수 선호도는 서로 독립적인 하이퍼파라미터 특성이라는 것이다. 학습률은 신경망 가중치 업데이트의 보폭을 결정하는 최적화 관련 파라미터인 반면, 할인 계수는 즉시 보상과 미래 보상 간의 중요도 균형을 조절하는 강화학습 고유의 파라미터이다 [32]. 따라서 A2C가 학습률에는 민감하면서도 높은 할인 계수를 선호하는 것은 각각 다른 측면의 알고리즘 특성을 나타내는 것이다.

이는 인간이 새로운 Atari 게임을 수 분에서 수 시간 내에 익히는 것과 대조적이다. 심지어 가장 효율적인 버전도 여전히 수십 시간의 플레이 시간에 해당하는 데이터가 필요하다.

5.3. MuJoCo 연속 제어 환경에서의 성능 비교#

5.3.1. OpenAI Spinning Up 벤치마크 결과#

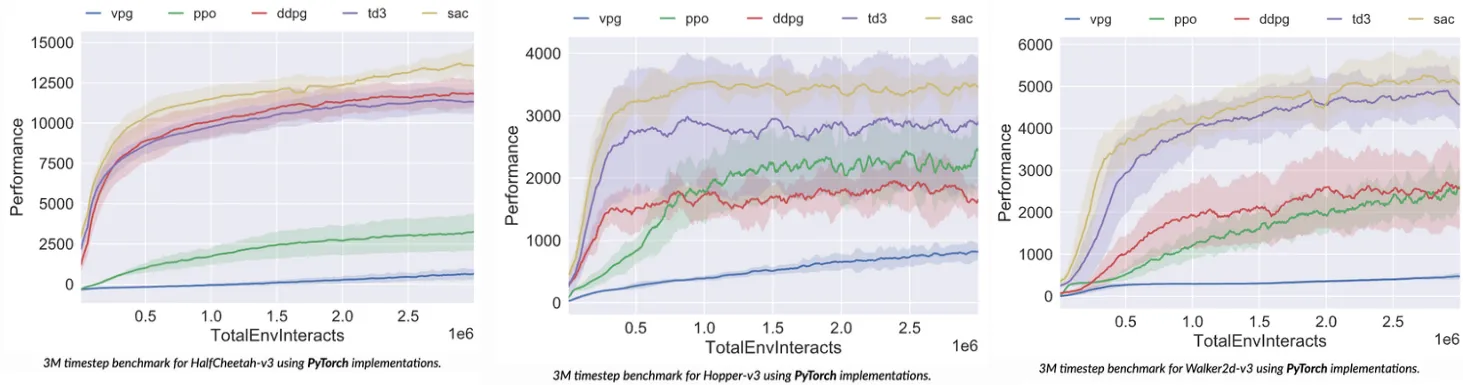
5.3.1.1. MuJoCo 환경 성능 비교#

HalfCheetah 환경에서는 SAC [22]가 PPO [3], DDPG [21], TD3 [23] 중에서도 제일 좋은 성능을 달성했다. 다른 알고리즘들과 다르게 PPO 알고리즘은 다른 알고리즘들에 비해서 성능이 굉장히 낮게 나온 것을 확인할 수 있다 [26].

Hopper 환경에서는 SAC가 다른 알고리즘들에 비해서 높은 성능을 보였고, 다음으로 TD3, PPO, DDPG 순으로 성능을 나타낼 수 있다 [26].

Walker2D 환경에서도 SAC가 가장 좋은 성능을 보였으며, 다음으로 TD3, DDPG, PPO 순으로 성능이 측정되었다 [26].

$\text{[그림 5.4] 강화학습 알고리즘별 MuJoCo 환경 OpenAI Spinning Up 벤치마크}$

5.3.2. Tianshou 벤치마크 결과#

Tianshou는 신뢰할 수 있고 재현 가능한 MuJoCo 벤치마크를 제공하며, 모든 실험은 1-10M 스텝에 걸쳐 10개의 랜덤 시드로 수행되었다 [27]. 다음은 주요 환경에서의 성능 비교 결과이다.

5.3.2.1. MuJoCo 환경 성능 비교#

HalfCheetah 환경에서 Tianshou 구현체의 성능을 살펴보면, SAC가 12138.8의 최고 성능을 기록했으며, 이는 원논문의 SAC 성능(~10400)과 Spinning Up 결과(~11520)보다 뛰어난 수치이다 [27]. TD3의 경우 10201.2의 성능을 보여 원논문(9637.0)과 유사한 수준이었다. PPO는 5783.9로 원논문 결과(~1800)보다 현저히 높은 성능을 달성했다.

Hopper 환경에서는 SAC가 3542.2의 성능으로 가장 우수했으며, TD3는 3472.2, PPO는 2609.3의 성능을 기록했다 [27]. 이는 앞선 OpenAI Spinning Up 결과와 유사한 패턴을 보여준다.

Walker2d 환경에서도 SAC가 5007.0으로 최고 성능을 달성했으며, TD3가 3982.4, PPO가 3588.5로 그 뒤를 이었다 [27].

$\text{[그림 5.5] 강화학습 알고리즘별 MuJoCo 환경 Tianshou 벤치마크}$

5.3.3. 알고리즘별 종합 성능 분석#

[그림 5.5]의 결과를 종합해보면 다음과 같은 특징을 확인할 수 있다 [27].

SAC(Soft Actor-Critic) 는 대부분의 연속 제어 환경에서 일관되게 최고 성능을 달성했다. 특히 HalfCheetah, Hopper, Walker2d, Ant 환경에서 다른 알고리즘 대비 우수한 결과를 보였다. 이는 SAC의 엔트로피 정규화와 off-policy 학습의 장점이 연속 제어 태스크에 효과적임을 시사한다 [22].

TD3(Twin Delayed Deep Deterministic Policy Gradient) 는 대부분의 환경에서 두 번째로 좋은 성능을 보였으며, 특히 복잡한 환경인 Ant에서 SAC에 근접한 성능을 달성했다. TD3의 target policy smoothing과 delayed policy update가 안정적인 학습에 기여한 것으로 판단된다 [23].

PPO(Proximal Policy Optimization) 는 on-policy 방법론 중에서는 양호한 성능을 보였으나, off-policy 방법론인 SAC와 TD3에 비해서는 상대적으로 낮은 성능을 기록했다. 그러나 Tianshou 구현체의 PPO는 원논문 결과보다 상당히 개선된 성능을 보여주었다 [3].

DDPG는 대부분의 환경에서 다른 알고리즘들에 비해 상대적으로 낮은 성능을 보였으며, 이는 DDPG의 높은 분산과 불안정성이 원인으로 분석된다 [21].

5.3.4. 런타임 성능 분석#

1M 타임스텝 기준 평균 런타임을 분석하면 [27]:

• SAC: 5.2시간으로 가장 오랜 시간이 소요되었으며, 업데이트 과정이 전체 시간의 83.8%를 차지했다.
• TD3: 3.3시간으로 두 번째로 긴 시간이 소요되었고, 업데이트가 81.7%를 차지했다.
• DDPG: 2.9시간으로 off-policy 방법론 중 가장 빠른 속도를 보였다.
• PPO: 24분으로 상당히 빠른 학습 속도를 보였으나, 64개의 병렬 환경을 사용한 결과이다.

5.3.5. OpenAI Spinning Up vs Tianshou 비교#

[그림 5.4]와 [그림 5.5]의 결과를 비교해보면, 전반적으로 SAC > TD3 > PPO > DDPG 순의 성능 순위는 일치한다 [26] [27]. 다만 구체적인 수치에서는 차이를 보이는데, 이는 하이퍼파라미터 설정, 구현 세부사항, 평가 방법론의 차이에 기인한다. Tianshou 구현체는 일반적으로 원논문 결과와 유사하거나 더 나은 성능을 보여주어 높은 신뢰성을 입증했다.

이러한 벤치마크 결과는 연속 제어 태스크에서 SAC와 TD3 같은 off-policy 방법론의 우수성을 명확히 보여주며, 특히 sample efficiency와 안정성 측면에서 on-policy 방법론 대비 뚜렷한 장점을 확인할 수 있다.

결과적으로 최고 성능이 필요한 경우 SAC를, 성능과 효율성의 균형이 중요한 경우 TD3를, 빠른 프로토타이핑이나 실시간 적용이 필요한 경우 PPO를 고려할 수 있다.

6. Challenges and Open Issues#

강화학습이 게임, 로보틱스, 자율주행 등 다양한 분야에서 좋은 성과를 거두었음에도 불구하고, 실제 세계의 복잡한 문제에 적용하기 위해서는 여전히 해결해야 할 근본적인 문제들이 존재한다. 본 섹션에서는 현재 강화학습 분야가 직면한 주요 도전과제들을 분석하고, 각 문제의 근본적인 원인과 해결을 위한 최신 연구 동향을 다룬다. 알겠습니다. 여러 각주를 배치할 때 개별적으로 표시하도록 수정하겠습니다.

6.1. 샘플 효율성의 근본적 한계#

6.1.1. 문제의 본질과 현황#

강화학습에서 가장 심각하고 지속적인 문제는 극도로 낮은 샘플 효율성이다. Zhang et al. (2024)은 “샘플 효율성 부족이 강화학습의 지속적인 도전과제”라고 강조하며, 특히 실제 응용에서 데이터 수집이 시간 소모적이고 비용이 많이 드는 상황에서 이 문제가 더욱 심각해진다고 보고했다 [33].

인간은 새로운 작업을 학습할 때 매우 적은 시행착오로도 효과적인 전략을 개발할 수 있지만, 현대의 강화학습 알고리즘들은 정말 많은 샘플들을 필요로 한다 [1].

이러한 비효율성의 근본 원인은 여러 층위에서 찾을 수 있다. 첫째, 강화학습은 본질적으로 시행착오를 기반으로 하기 때문에 최적 정책을 찾기 위해서는 상당한 탐험이 필요하다. 둘째, 현재의 알고리즘들은 대부분 각 경험을 독립적으로 처리하며, 경험 간의 구조적 관계나 패턴을 효과적으로 활용하지 못한다. 셋째, 희소한 보상 신호로 인해 의미 있는 학습 신호를 얻기까지 오랜 시간이 걸린다 [32].

6.1.2. 최신 해결 방향#

샘플 효율성 문제 해결을 위한 최신 연구들은 여러 방법을 제시하고 있다. Zhang et al. (2024)은 LLM(Large Language Model)으로부터 배경 지식을 추출하여 보상 형성(reward shaping)에 활용하는 프레임워크를 제안했다. 이 방법은 환경에 대한 일반적 이해를 제공하여 다양한 하위 강화학습 작업이 일회성 지식 표현으로부터 혜택을 받을 수 있게 한다. 실험 결과, Minigrid와 Crafter 도메인의 다양한 하위 작업에서 상당한 샘플 효율성 개선을 달성했다 [33].

EfficientZero V2 프레임워크는 MCTS와 모델 기반 계획을 결합하여 이산 및 연속 제어 작업 모두에서 우수한 성능을 보였다. 이러한 방법들은 시각적 입력과 저차원 입력이 모두 있는 환경에서 정밀한 제어와 의사결정을 가능하게 한다 [38].

6.1.3. 실제 응용에서의 제약과 해결책#

실제 세계 응용에서 샘플 비효율성은 심각한 제약을 가져온다 [1]. 로보틱스 분야에서는 물리적 로봇이 수백만 번의 시행착오를 반복하는 것이 현실적으로 불가능하다. 이러한 시행착오는 막대한 시간과 비용을 요구할 뿐만 아니라 장비 손상의 위험도 동반한다. 자율주행에서는 안전하지 않은 행동으로 인한 사고 가능성 때문에 실제 환경에서의 광범위한 학습이 제한된다.

최근 연구들은 이러한 제약을 극복하기 위해 메타 러닝, 전이 학습, 그리고 시뮬레이션-실제 전이 기법의 개발에 집중하고 있다. 특히 계층적 강화학습과 목표 조건부 강화학습을 통해 추상적 행동 표현을 학습하여 샘플 효율성을 크게 개선할 수 있음이 보고되고 있다 [36].

6.2. 안전성과 신뢰성 문제#

6.2.1. 안전 제약 하에서의 학습#

안전한 강화학습은 특정 안전 제약을 만족하면서 기대 누적 보상을 최대화하는 제약 기준을 기반으로 한다. 제약 표현의 다양성과 이들 간의 상호관계에 대한 탐구 부족으로 인해 이 분야의 체계적 이해는 여전히 어려운 상황이다.

안전 강화학습의 핵심 도전과제는 탐험 과정에서 안전 제약을 위반하지 않으면서도 효과적인 학습을 수행하는 것이다 [34]. Mazumdar et al. (2024)은 학습 단계에서 안전 제약을 위반하지 않는 온라인 강화학습 알고리즘을 제시했다 [34]. 이들은 상태 공간을 금기 집합(taboo set), 금지 집합(forbidden set), 목표 집합(target set)으로 분할하고, 높은 신뢰도로 안전한 정책을 학습하는 방법을 제안했다 [34].

6.2.2. 확률적 안전 보장#

전통적인 안전 강화학습은 기댓값에만 제약을 설정하고 분포의 꼬리 부분을 무시하는 경우가 많아서 위험할 수 있다 [34].

확률적 제약을 위한 안전 정책 기울기(Safe Policy Gradient) 방법들이 개발되어, 높은 확률로 에이전트의 궤적을 주어진 안전 집합 내에 유지하는 정책을 학습할 수 있게 되었다. 이러한 방법들은 정책 기반 알고리즘을 넘어 다양하게 적용될 수 있는 범용성을 제공한다.

6.3. 다중 에이전트 환경의 복잡성#

6.3.1. 비정상성과 확장성 문제#

다중 에이전트 강화학습(MARL, Multi Agent Reinforcement Learning)에서 가장 중요한 도전과제는 환경의 비정상성이다. 각 에이전트의 학습이 다른 에이전트들의 정책 변화에 영향을 받기 때문에 단일 에이전트 강화학습의 기본 가정이 위배된다. 이는 단일 에이전트 알고리즘을 여러 에이전트에 직접 적용했을 때 최적 해로 수렴하지 못하는 주된 원인이다 [37].

확장성은 MARL의 또 다른 핵심 도전과제로, 높은 수의 에이전트가 관련된 실제 문제에 적용될 수 있는 알고리즘 개발이 필수적이다. 대부분의 기존 방법들은 제한된 수의 에이전트에서만 수용 가능한 성능을 유지할 수 있다 [37].

6.3.2. 협력과 경쟁의 균형#

현실 세계의 많은 응용은 협력과 경쟁이 동시에 존재하는 혼합 환경이다. 게임 이론과 기계학습의 관점을 통합하여 데이터 주도 학습 과정을 통해 지능적 사회 에이전트의 바람직한 행동 특성을 부여하는 것이 중요하다 [37].

물환경 시스템에서의 MARL 응용 연구는 제한된 자원, 시스템 이질성, 불안정한 통신 등의 실질적 제약이 있는 상황에서 전역 협력 효율성을 개선하는 도전과제와 해결책을 제시했다. 특히 도시 배수 시스템, 급수 시스템, 수력 발전 시스템 등에서 실시간 조절이 요구되는 복잡한 실제 시스템에서의 효과성 평가가 필요한 상황이다.

6.3.3. 통신과 조정 문제#

그리드 상호작용 건물에서의 MARL 연구는 실제 세계 제약 조건들을 체계화했다. 통신 제약, 부분 관측성, 그리고 에이전트 간 정보 공유가 전체 시스템 성능에 미치는 영향을 분석했다 [37]. 연구 결과, 최적화된 규칙 기반 제어기로부터의 더 긴 오프라인 훈련이 장기적으로 성능 향상을 가져오는 것으로 나타났다.

6.4. 일반화와 전이학습의 한계#

6.4.1. Sim-to-Real 간극#

시뮬레이션에서 훈련된 정책을 실제 환경에 적용할 때 발생하는 성능 저하는 강화학습의 실용화에 있어 가장 큰 장벽 중 하나이다. 물리 법칙, 센서 노이즈, 예측 불가능한 외부 요인 등으로 인해 시뮬레이션과 현실 사이에는 상당한 차이가 존재한다 [1].

도메인 랜덤화(Domain Randomization) 기법들이 이 문제 해결을 위해 제안되었으나, 여전히 한계가 있다. 자동 도메인 랜덤화(Automatic Domain Randomization)와 같은 더 고급 방법들이 개발되고 있지만, 복잡한 실제 환경의 모든 변동성을 포착하는 것은 여전히 어려운 과제이다.

6.4.2. 분포 변화와 적응성#

훈련 시의 상태 분포와 테스트 시의 상태 분포가 다르면 성능이 크게 저하되는 분포 변화(distribution shift) 문제는 특히 심각하다. 현실 세계의 환경은 끊임없이 변화하며 예측하기 어려운 요소들을 포함하므로, 강화학습 에이전트는 이러한 변화에 빠르게 적응할 수 있어야 된다.

메타 러닝과 지속적 학습(continual learning) 기법들이 이 문제를 해결하기 위해 연구되고 있으나, 여전히 만족스러운 해결책은 없는 상태이다. 특히 catastrophic forgetting 문제와 새로운 작업에 대한 빠른 적응 사이의 균형을 맞추는 것이 중요한 과제로 남아있다.

6.5. 계산 효율성과 확장성#

6.5.1. 고차원 공간에서의 학습#

계층적 모델 기반 강화학습(HMBRL, Hierarchical Model-Based Reinforcement Learning)은 모델 기반 강화학습의 샘플 효율성과 계층적 강화학습의 추상화 능력을 결합하려고 시도한다 [36]. 그러나 현재 접근법들의 구조적, 개념적 복잡성으로 인해 일반적 원칙을 추출하기 어려워 새로운 사용 사례에 대한 이해와 적응이 제한되고 있다 [36].

강화학습은 상태 공간과 행동 공간의 크기가 증가함에 따라 지수적으로 복잡해지는 차원의 저주 문제에 직면한다. 고차원 상태 공간에서는 효과적인 탐험이 극도로 어려워지며, 의미 있는 학습 신호를 얻기 위해 필요한 샘플 수가 기하급수적으로 증가한다 [32].

6.5.2. 실시간 처리 요구사항#

자율주행, 인터넷 거래 등 많은 실제 응용에서는 실시간 의사결정이 요구된다. 하지만 현재의 강화학습 알고리즘들, 특히 깊은 신경망을 사용하는 방법들은 이러한 실시간 요구사항을 만족시키기 어렵다. 더 나아가 엣지 디바이스나 모바일 환경에서는 제한된 계산 자원과 배터리 수명 때문에 복잡한 알고리즘을 사용하기 어렵다. 이러한 환경에서 동작할 수 있는 경량화된 강화학습 알고리즘의 개발이 필요하지만, 성능과 효율성 사이의 균형을 맞추는 것은 여전히 어려운 과제이다.

6.6. 이론적 한계와 보장#

6.6.1. 수렴성과 안정성#

딥러닝을 사용하는 현대의 많은 강화학습 방법들은 이론적 수렴성 보장이 없다. 수렴성, 안정성, 그리고 탐험-활용 딜레마와 같은 일반적인 도전과제들이 여전히 해결되지 않은 상태이다 [36].

DQN과 같은 함수 근사 방법들은 실증적으로는 잘 작동하지만, 수학적으로는 발산할 가능성을 배제할 수 없다 [4] [4-1]. 비선형 함수 근사, 경험 리플레이, 타겟 네트워크 등의 기법들이 결합되면서 이론적 분석이 더욱 어려워졌다.

6.6.2. 근사 오차와 최적성#

함수 근사를 사용하는 강화학습에서는 근사 오차가 불가피하게 발생한다. 이러한 오차가 학습 과정에서 어떻게 누적되고 최종 성능에 어떤 영향을 미치는지에 대한 이론적 이해가 부족하다. 특히 깊은 신경망의 경우 근사 능력이 뛰어나지만 이론적 분석이 굉장히 어렵다 [25].

6.7. 미래 연구 방향과 해결 전략#

6.7.1. LLM과의 융합#

LLM의 광범위한 사전 훈련된 지식과 고수준 일반 능력(High-Level General Abilities, 기본적인 능력)을 활용하여 다중 작업 학습, 샘플 효율성, 고수준 작업 계획 등의 측면에서 강화학습을 강화하는 연구가 활발히 진행되고 있다 [33]. LLM을 정보 처리기, 보상 설계자, 의사결정자, 생성자의 역할로 분류하여 체계적으로 활용하는 방법론이 제시되고 있다.

6.7.2. 통합적 접근법#

이러한 근본적 도전과제들을 해결하기 위해서는 다각도의 접근이 필요하다.

메타 러닝과 전이 학습을 통한 샘플 효율성 개선, 안전한 탐험을 위한 제약 기반 강화학습, 그리고 해석 가능한 의사결정을 위한 인과적 추론 방법의 개발이 중요할 것이다 [35]. 이론적 측면에서 더욱 발전하기 위해서는 함수 근사를 사용하는 강화학습의 수렴성 분석, 다중 에이전트 환경에서의 균형점 특성 연구, 그리고 부분 관측 환경에서의 최적 정책 특성 규명이 필요하다 [32]. 또한 인간의 가치와 선호도를 효과적으로 통합하는 방법론과 편향을 줄이고 공정성을 보장하는 기법의 개발 또한 중요하다 [35]. 더 나아가 실용적 측면에서는 더욱 현실적인 벤치마크 환경의 개발, 시 뮬레이션과 현실 간의 차이를 줄이는 domain adaptation 기법, 그리고 실시간 제약 하에서 동작하는 경량화된 알고리즘의 개발 실용적인 발전을 위해 필요하다 [1].

앞서 말한 다양한 노력을 통해 강화학습이 실제 세계의 문제들을 잘 해결할 수 있는 성숙한 기술로 발전할 수 있을 것이라 기대한다.

7. Future Research Directions#

강화학습 분야는 현재 전례 없는 변화의 시기를 맞고 있다. 특히 2025년에 등장한 DeepSeek-R1 [11]은 강화학습이 추론 능력 향상에 얼마나 효과적인지를 보여주는 중요한 이정표가 되었다. 본 섹션에서는 이러한 최신 연구 동향을 중심으로 강화학습의 미래 연구 방향을 분석한다.

7.1. Large Language Models와의 융합#

7.1.1. 순수 강화학습을 통한 추론 능력 개발#

최근 연구 성과로 주목받은 DeepSeek-R1 [11]에서 가장 주목할 점은 DeepSeek-R1-Zero가 감독 학습 없이 순수한 강화학습만으로 뛰어난 추론 능력을 개발했다는 것이다. 흥미롭게 볼만한 곳은 모델이 스스로 자기 검증(self-verification), 반성(reflection), LCOT(Long Chain-Of-Thought) 등의 복잡한 추론 행동을 강화학습을 통해 자연스럽게 학습할 수 있음을 시사한다.

$\text{[그림 6.1] Deepseek 성능지표}$

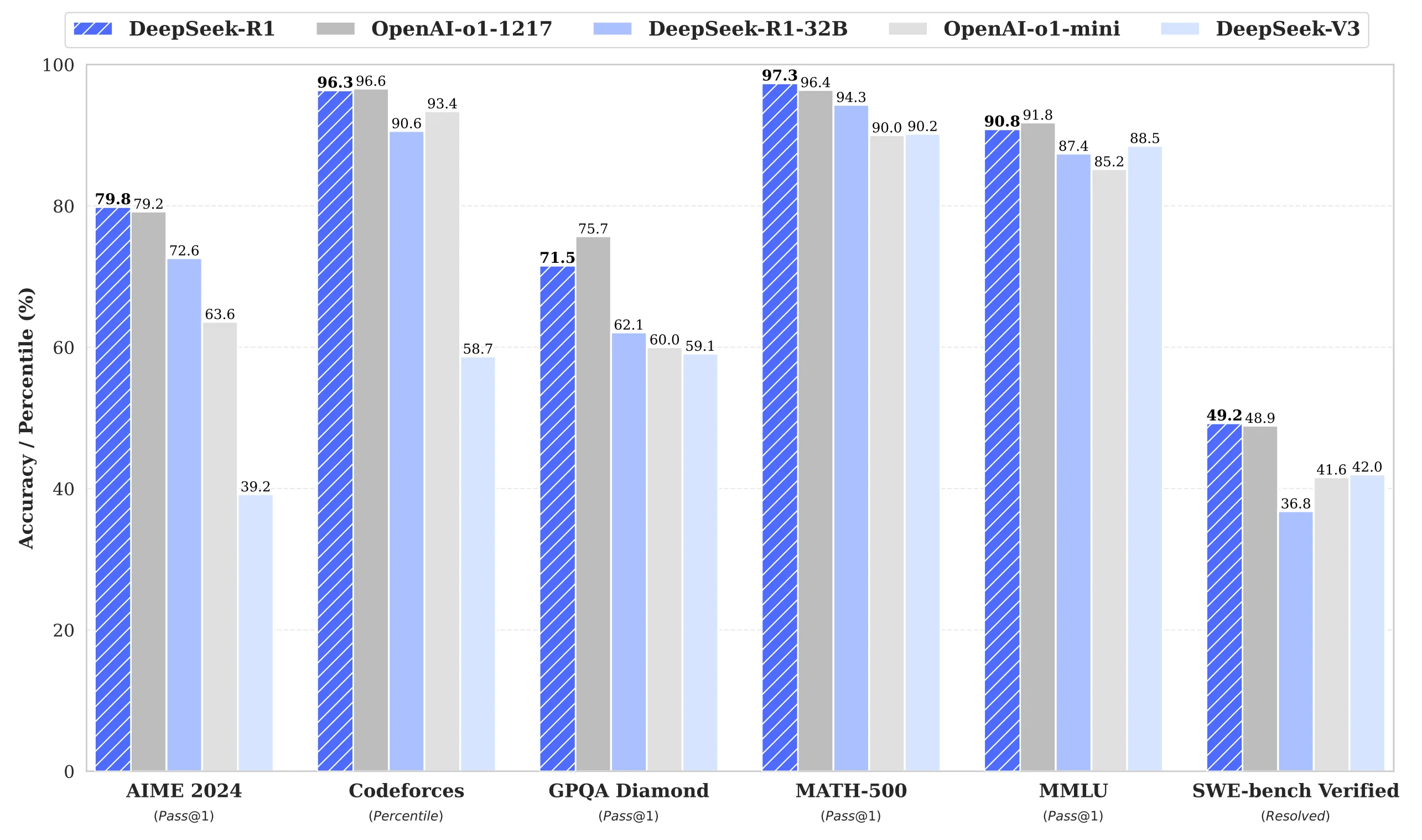
7.1.2. DeepSeek-R1의 성능#

DeepSeek-R1 [11]의 등장으로 LLM 생태계의 큰 변화가 온 것은 단지 성능 때문만이 아니다. 비용 효율성 측면에서 DeepSeek-R1은 API 이용료가 입력 토큰당 $0.55, 출력 토큰당 $2.19로 OpenAI o1의 입력 토큰당 $15, 출력 토큰당 $60에 비해 90-95% 저렴한 비용를 보여주었다 [28]. 이는 강화학습 기반 추론 모델의 상용화에 있어 큰 발전이며, 중요한 진전이다.

7.1.3. GRPO(Group Relative Policy Optimization)의 도입#

DeepSeek-R1 [11]은 기존의 Proximal Policy Optimization (PPO) [3] 대신 Group Relative Policy Optimization (GRPO)을 사용했다. 이를 통해서 수학적 추론 능력을 크게 향상시켰으며, 향후 강화학습 기반 언어 모델 훈련의 새로운 방향을 제시했다.

7.2. 다중 에이전트 강화학습의 진화#

7.2.1. 대규모 시스템에서의 협력과 경쟁#

다중 에이전트 강화학습(MARL) [37]은 DeepSeek-R1과는 다른 방향으로 발전하고 있지만, 마찬가지로 중요한 연구 영역이다. 특히 수환경 시스템의 지능형 자동화와 제어에서 상당한 응용 잠재력을 보여주고 있으며, 복잡한 시스템에서 협력 제어, 정책 최적화, 작업 할당 문제를 해결하는 데 활용되고 있다. 물 공급 스케줄링, 수력-에너지 공동 조절, 자율 모니터링 등의 핵심 작업에서 모델링 메커니즘과 정책 조정 전략이 활발히 연구되고 있다.

7.3. 로보틱스 분야의 실용화#

7.3.1. 다양한 로봇 플랫폼에서의 성과#

로보틱스 분야에서 강화학습은 사족 보행, 드론 내비게이션, 바퀴형 로봇, 객체 조작 등 다양한 영역에서 기계가 동적 환경에 적응하고 성능을 최적화할 수 있게 하고 있다. 최근 연구에서는 딥 강화학습이 실제 로봇 시스템에서 달성한 성공 사례들을 체계적으로 분석하고 있다 [1]. 안정적이고 샘플 효율적인 실세계 강화학습 패러다임의 필요성, 복잡한 장기간 개방형 작업을 다루기 위한 다양한 역량의 발견과 통합을 위한 전체론적 접근법이 강조되고 있다.

7.3.2. Sim-to-Real 전이와 안전성#

시뮬레이션에서 실제 세계로의 전이 문제는 여전히 로보틱스 강화학습의 핵심 과제이다. 최근 연구들은 동역학 무작위화(dynamics randomization)를 사용하여 시뮬레이션에서 순환 정책을 훈련하고 이를 물리적 로봇에 직접 배포하는 방법들을 제안하고 있다. 하지만 복잡한 실제 환경의 모든 변수들을 고려하는 것은 여전히 어려운 과제이다.

안전한 탐험(Safe Exploration)은 실제 로봇 응용에서 매우 중요한 연구 영역이다 [34]. 특히 자율주행차나 의료용 로봇과 같이 안전이 중요한 시스템에서는 학습 과정에서도 안전을 보장해야 한다. 제약 기반 강화학습과 안전 크리틱 방법들이 활발히 연구되고 있으며, 이는 로보틱스 분야의 실용화에 필수적인 요소로 자리잡고 있다.

7.4. 미래 연구 방향#

7.4.1. 오픈소스의 영향력과 연구 생태계 변화#

DeepSeek-R1의 오픈소스 공개는 강화학습 연구 생태계에 중대한 변화를 가져왔다. MIT 라이선스 하에 공개된 이 모델은 상업적 사용이 자유롭고, 모델 가중치뿐만 아니라 전체 훈련 과정까지 공개되어 있다.

Hugging Face CEO에 따르면 공개 후 며칠 만에 500개 이상의 파생 모델이 생성되고 250만 번 다운로드되었다고 한다. 이는 원본 모델 다운로드의 5배에 해당하는 수치로, 오픈소스 AI의 분산화된 혁신력을 보여준다.

7.4.2. 데이터와 컴퓨팅 패러다임의 전환#

DeepSeek-R1은 더 많은 데이터에서 더 똑똑한 컴퓨팅으로의 패러다임 전환을 보여준다. 전통적인 감독 학습이 대량의 라벨링된 데이터셋에 의존하는 반면, 강화학습은 상호작용과 피드백을 통한 학습으로 데이터 프라이버시와 편향 문제를 완화할 수 있다.

특히 두 모델 훈련 과정에서 첫 번째 모델이 RL을 통해 추론 궤적을 생성하고, 이를 선별적으로 사용하여 두 번째 모델을 훈련하는 방식은 데이터 양보다 질을 중시하는 효율적 접근법을 제시한다.

7.4.3. 투명성과 해석가능성의 진전#

DeepSeek-R1은 reasoning traces를 통해 의사결정 과정을 단계별로 공개한다. 이는 의료진이 AI 진단의 근거를 이해하고 더 나은 치료 결정을 내리는 데 도움이 될 수 있다. OpenAI의 “블랙박스” 모델들과 달리, DeepSeek-R1의 오픈소스 프레임워크와 명시적인 추론 경로는 상용 모델에서는 일반적으로 제한되는 수준의 검토와 커스터마이징을 가능하게 한다. 이는 해석할 수 없던 LLM 생태계에서 강화학습의 강력함을 보여주는 좋은 사례이다.

앞으로 강화학습은 더 이상 게임이나 단순한 제어 문제에 국한되지 않고, 추론, 창의성, 복잡한 문제 해결이 필요한 인지적 작업의 핵심 기술로 자리잡을 것으로 기대된다. DeepSeek-R1이 보여준 순수 강화학습을 통한 추론 능력, MARL의 대규모 시스템 제어 가능성, 그리고 로보틱스의 실세계 적용 성과들은 미래 강화학습 연구의 무한한 가능성을 현실로 만드는 중요한 발판이 되고있다.

8. Conclusion#

본 논문에서는 강화학습의 전반적 이론을 다루면서 최신 연구 동향까지 분석했다. 동적 계획법[30]에서 시작된 강화학습은 Q-Learning[2], DQN[4]을 거쳐 인간에게 승리를 거둔 AlphaGo[9]를 넘어 LLM의 기술적 혁신까지 지속적으로 발전해왔다.

인간의 학습 방식과 유사하게 시행착오를 통해 최적의 전략을 찾아 나간다는 강화학습의 근본적인 아이디어는 다른 기계학습 패러다임과 차별화되는 지점이다. 최근 인공지능 분야에서 블랙박스 모델들이 많이 등장하는 반면, 강화학습은 마르코프 결정 과정(MDP)과 벨만 방정식[30] 등 명확한 수학적 프레임워크에 기반하여 의사결정의 원리를 설명하려는 노력을 지속하고 있다. 이러한 해석 가능성에 대한 탐구는 강화학습을 더욱 흥미롭고 신뢰할 수 있는 학문 분야로 만든다.

강화학습은 여전히 샘플 효율성[33], 안전성[34]과 같은 현실적인 도전과제들을 마주하고 있다. 그러나 스스로 목표를 설정하고 상호작용을 통해 학습하는 능력은 미래 인공지능의 핵심이 될 잠재력을 품고 있다.

궁극적으로 인공지능이 더욱 복잡하고 자율적인 과제를 수행해야 하는 시점이 오면, 목표지향적 의사결정을 위한 가장 원칙적인 접근법인 강화학습이 기술 발전의 중심에 서게 될 것이다. 본 연구에서 고찰한 바와 같이, 강화학습은 인공지능의 미래를 이끌어갈 핵심 동력으로 자리매김할 것으로 기대한다.

Reference#

---

[1] C. Tang, B. Abbatematteo, J. Hu, R. Chandra, R. Martín-Martín, and P. Stone, “Deep Reinforcement Learning for Robotics: A Survey of Real-World Successes,” arXiv preprint arXiv:2408.03539, Aug. 2024. [Online]. Available: https://arxiv.org/abs/2408.03539

[2] C. J. C. H. Watkins and P. Dayan, “Technical Note: Q-Learning,” Machine Learning, vol. 8, no. 3, pp. 279-292, May 1992, doi: 10.1023/A:1022676722315.

[3] J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal Policy Optimization Algorithms,” arXiv preprint arXiv:1707.06347, Jul. 2017. [Online]. Available: https://arxiv.org/abs/1707.06347

[4] V. Mnih et al., “Playing Atari with Deep Reinforcement Learning,” arXiv preprint arXiv:1312.5602, Dec. 2013. [Online]. Available: https://arxiv.org/abs/1312.5602

[4-1] V. Mnih et al., “Human-level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529-533, Feb. 2015, doi: 10.1038/nature14236.

[5] H. van Hasselt, A. Guez, and D. Silver, “Deep Reinforcement Learning with Double Q-learning,” arXiv preprint arXiv:1509.06461, Sep. 2015. [Online]. Available: https://arxiv.org/abs/1509.06461

[6] Z. Wang, T. Schaul, M. Hessel, H. van Hasselt, M. Lanctot, and N. de Freitas, “Dueling Network Architectures for Deep Reinforcement Learning,” arXiv preprint arXiv:1511.06581, Nov. 2015. [Online]. Available: https://arxiv.org/abs/1511.06581

[7] M. Hessel et al., “Rainbow: Combining Improvements in Deep Reinforcement Learning,” in Proc. 32nd AAAI Conf. Artif. Intell., New Orleans, LA, USA, Feb. 2018, pp. 3215-3222. [Online]. Available: https://arxiv.org/abs/1710.02298

[8] D. Ha and J. Schmidhuber, “World Models,” arXiv preprint arXiv:1803.10122, Mar. 2018. [Online]. Available: https://arxiv.org/abs/1803.10122

[9] D. Silver et al., “Mastering the game of Go with deep neural networks and tree search,” Nature, vol. 529, no. 7587, pp. 484-489, Jan. 2016, doi: 10.1038/nature16961.

[10] K. Chua, R. Calandra, R. McAllister, and S. Levine, “Deep Reinforcement Learning in a Handful of Trials using Probabilistic Dynamics Models,” in Proc. 35th Int. Conf. Machine Learning (ICML), Stockholm, Sweden, Jul. 2018, pp. 1006-1015. [Online]. Available: https://arxiv.org/abs/1805.12114

[11] DeepSeek-AI, “DeepSeek-R1: Incentivizing reasoning capability in LLMs via reinforcement learning,” arXiv preprint arXiv:2501.12948, Jan. 2025. [Online]. Available: https://arxiv.org/abs/2501.12948

[12] D. E. Rumelhart, G. E. Hinton, and R. J. Williams, “Learning representations by back-propagating errors,” Nature, vol. 323, no. 6088, pp. 533-536, Oct. 1986. [Online]. Available: https://www.nature.com/articles/323533a0

[13] D. P. Kingma and M. Welling, “Auto-encoding variational bayes,” arXiv preprint arXiv:1312.6114, Dec. 2013. [Online]. Available: https://arxiv.org/abs/1312.6114

[14] D. Silver, J. Schrittwieser, K. Simonyan, I. Antonoglou, A. Huang, A. Guez, T. Hubert, L. Baker, M. Lai, A. Bolton, Y. Chen, T. Lillicrap, F. Hui, L. Sifre, G. van den Driessche, T. Graepel, and D. Hassabis, “Mastering the game of Go without human knowledge,” Nature, vol. 550, no. 7676, pp. 354-359, Oct. 2017. [Online]. Available: https://www.nature.com/articles/nature24270

[15] R. S. Sutton, “Dyna, an integrated architecture for learning, planning, and reacting,” SIGART Bull., vol. 2, no. 4, pp. 160-163, Jul. 1990. [Online]. Available: https://dl.acm.org/doi/10.1145/122344.122377

[16] M. P. Deisenroth and C. E. Rasmussen, “PILCO: A model-based and data-efficient approach to policy search,” in Proc. 28th Int. Conf. Machine Learning (ICML), Bellevue, WA, USA, Jun. 2011, pp. 465-472. [Online]. Available: https://dl.acm.org/doi/10.5555/3104482.3104541

[17] J. Schrittwieser, I. Antonoglou, T. Hubert, K. Simonyan, L. Sifre, S. Schmitt, A. Guez, E. Lockhart, D. Hassabis, T. Graepel, T. Lillicrap, and D. Silver, “Mastering Atari, Go, chess and shogi by planning with a learned model,” Nature, vol. 588, no. 7839, pp. 604-609, Dec. 2020. [Online]. Available: https://www.nature.com/articles/s41586-020-03051-4

[18] R. J. Williams, “Simple statistical gradient-following algorithms for connectionist reinforcement learning,” Machine Learning, vol. 8, no. 3-4, pp. 229-256, May 1992. [Online]. Available: https://link.springer.com/article/10.1007/BF00992696

[19] J. Schulman, S. Levine, P. Abbeel, M. Jordan, and P. Moritz, “Trust region policy optimization,” in Proc. 32nd Int. Conf. Machine Learning (ICML), Lille, France, Jul. 2015, pp. 1889-1897. [Online]. Available: https://arxiv.org/abs/1502.05477

[20] V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. P. Lillicrap, T. Harley, D. Silver, and K. Kavukcuoglu, “Asynchronous methods for deep reinforcement learning,” in Proc. 33rd Int. Conf. Machine Learning (ICML), New York, NY, USA, Jun. 2016, pp. 1928-1937. [Online]. Available: https://arxiv.org/abs/1602.01783

[21] T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, and D. Wierstra, “Continuous control with deep reinforcement learning,” arXiv preprint arXiv:1509.02971, Sep. 2015. [Online]. Available: https://arxiv.org/abs/1509.02971

[22] T. Haarnoja, A. Zhou, P. Abbeel, and S. Levine, “Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor,” in Proc. 35th Int. Conf. Machine Learning (ICML), Stockholm, Sweden, Jul. 2018, pp. 1861-1870. [Online]. Available: https://arxiv.org/abs/1801.01290

[23] S. Fujimoto, H. van Hoof, and D. Meger, “Addressing function approximation error in actor-critic methods,” in Proc. 35th Int. Conf. Machine Learning (ICML), Stockholm, Sweden, Jul. 2018, pp. 1587-1596. [Online]. Available: https://arxiv.org/abs/1802.09477

[24] N. De La Fuente and D. A. Vidal Guerra, “A comparative study of deep reinforcement learning models: DQN vs PPO vs A2C,” arXiv preprint arXiv:2407.14151, July 2024. [Online]. Available: https://arxiv.org/abs/2407.14151

[25] K. O’Shea and R. Nash, “An Introduction to Convolutional Neural Networks,” arXiv preprint arXiv:1511.08458, Dec. 2015. [Online]. Available: https://arxiv.org/abs/1511.08458

[26] “Benchmarks for Spinning Up Implementations,” OpenAI, [Online]. Available: https://spinningup.openai.com/en/latest/spinningup/bench.html#halfcheetah-pytorch-versions. [Accessed: Aug. 19, 2025].

[27] “Benchmark — Tianshou 0.4.8 documentation,” Tianshou, [Online]. Available: https://tianshou.org/en/v0.4.8/tutorials/benchmark.html#mujoco-benchmark. [Accessed: Aug. 19, 2025].

[28] “DeepSeek R1 vs OpenAI o1: Installation, Features, Pricing,” MeetCody.ai, Jan. 23, 2025. [Online]. Available: https://meetcody.ai/blog/deepseek-r1-open-source-installation-features-pricing/. [Accessed: Aug. 19, 2025].

[29] L. Kocsis and C. Szepesvári, “Bandit based Monte-Carlo planning,” in Proc. 17th Eur. Conf. Machine Learning (ECML), Berlin, Germany, Sep. 2006, pp. 282-293.

[30] R. Bellman, Dynamic Programming. Princeton, NJ, USA: Princeton University Press, 1957.

[31] M. Toromanoff, E. Wirbel, and F. Moutarde, “Is Deep Reinforcement Learning Really Superhuman on Atari? Leveling the playing field,” arXiv preprint arXiv:1908.04683, Aug. 2019. [Online]. Available: https://arxiv.org/abs/1908.04683

[32] R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction, 2nd ed. Cambridge, MA, USA: MIT Press, 2018.

[33] F. Zhang, J. Li, Y.-C. Li, Z. Zhang, Y. Yu, and D. Ye, “Improving Sample Efficiency of Reinforcement Learning with Background Knowledge from Large Language Models,” arXiv preprint arXiv:2407.03964, Jul. 2024. [Online]. Available: https://arxiv.org/abs/2407.03964

[34] A. Mazumdar, R. Wisniewski, and M. L. Bujorianu, “Safe Reinforcement Learning for Constrained Markov Decision Processes with Stochastic Stopping Time,” arXiv preprint arXiv:2403.15928, Mar. 2024. [Online]. Available: https://arxiv.org/abs/2403.15928

[35] “Open Problems and Fundamental Limits of Reinforcement Learning from Human Feedback,” arXiv preprint arXiv:2411.18892, Nov. 2024. [Online]. Available: https://arxiv.org/abs/2411.18892

[36] A. Mohan, A. Jain, and M. Mausam, “Structure in Deep Reinforcement Learning: A Survey and Open Problems,” arXiv preprint arXiv:2306.16021, Jun. 2023. [Online]. Available: https://arxiv.org/abs/2306.16021

[37] D. Huh and P. Mohapatra, “Multi-agent Reinforcement Learning: A Comprehensive Survey,” arXiv preprint arXiv:2312.10256, Dec. 2023. [Online]. Available: https://arxiv.org/abs/2312.10256

[38] S. Wang, S. Liu, W. Ye, J. You, and Y. Gao, “EfficientZero V2: Mastering Discrete and Continuous Control with Limited Data,” in Proc. 41st Int. Conf. Machine Learning (ICML), Vienna, Austria, Jul. 2024, pp. 51225-51268. [Online]. Available: https://arxiv.org/abs/2403.00564

[39] W. Duvaud, “MuZero General Implementation,” GitHub repository, 2021. [Online]. Available: https://github.com/werner-duvaud/muzero-general. [Accessed: 19-Aug-2025].